Analyse Procrustéenne Généralisée

Principe de l’analyse procrustéenne généralisée

L'analyse procrustéenne généralisée (Generalised Procrustes Analysis ou GPA en anglais) est une méthode mathématique qui permet de réaliser des transformations sur des tableaux multidimensionnels de manière à réduire la distance euclidienne entre ces tableaux.

Utilisation de l’analyse procrustéenne généralisée en analyse sensorielle

L'analyse procrustéenne généralisée est souvent utilisée en analyse sensorielle en préalable à une cartographie des préférences (Preference mapping) par exemple pour réduire les effets d'échelles et pour aboutir à une configuration consensuelle. Elle peut aussi permettre d'analyser la proximité de certains termes utilisés par différents experts.

Calcul de l’analyse procrustéenne généralisée

On désigne par configuration une matrice n x p (n objets, p dimensions) correspondant à la description de n objets (ou individus / produits) suivant p dimensions (ou attributs/ variables / critères / descripteurs).

On appelle configuration consensuelle la configuration moyenne calculée à partir des m configurations. L'analyse procrustéenne généralisée est une méthode itérative qui permet de réduire par une suite de transformations des m configurations (changement d'échelle, translations, rotations, réflexions), la distance des m configurations à la configuration consensuelle, cette dernière évoluant après chaque transformation.

Prenons l'exemple de 5 experts notant 4 fromages suivant 3 critères, les notes pouvant aller de 1 à 10. On peut facilement envisager qu'un sujet ait tendance à être plus dur dans sa notation, entraînant un décalage vers le bas des notes, ou qu'un autre ait tendance à mettre des notes autour de la moyenne, sans oser se risquer à utiliser des notes extrêmes. Travailler sur une configuration moyenne risquerait alors d'entraîner de fausses interprétations. On comprend aisément qu'une translation des notes du premier sujet est nécessaire, ou qu'une remise à l'échelle des notes du second sujet rendrait les notes de ce dernier éventuellement plus proches de celles des autres sujets.

Une fois la configuration consensuelle obtenue, il est possible de réaliser une analyse en composantes principales (ACP) de manière à permettre une visualisation optimale en deux ou trois dimensions des configurations après transformation et de la configuration consensuelle. XLSTAT-MX réalise une ACP non normée et affiche le cercle des corrélations et la carte des objets.

Il existe deux cas différents :

1. Si le nombre et la désignation des p dimensions sont identiques pour les m configurations, on parle en analyse sensorielle de profils conventionnels.
2. Si le nombre p et la désignation des dimensions varie d'une configuration à l'autre, on parle en analyse sensorielle de profils libres, et les données ne peuvent alors être représentées que sous la forme d'une suite de m matrices de taille n x p(k), k=1,2, …, m.

Algorithmes pour l’analyse procrustéenne généralisée dans XLSTAT

XLSTAT est le seul logiciel offrant le choix entre les deux principaux algorithmes disponibles :

1. Le premier fondé sur les travaux initiés par John Gower (1975),
2. et le second basé sur les travaux de Jacques Commandeur (1991).

En fonction du jeu de données, l'un ou l'autre algorithme sera le plus performant (en termes de moindres carrés), mais l'algorithme de Commandeur a la particularité de permettre de prendre en compte des données manquantes. Par données manquantes, on entend ici que pour une configuration donnée et une observation donnée, les valeurs n'ont pas été enregistrées pour toutes les dimensions de la configuration. Ce dernier cas peut se produire en analyse sensorielle, si l'un des sujets n'a pas évalué d'un produit.

Résultats pour l’analyse procrustéenne généralisée dans XLSTAT

Tableau de PANOVA

Le tableau PANOVA est inspiré du format du tableau d'analyse de la variable du modèle linéaire, ce tableau permet d'évaluer l'apport respectif des différentes transformations. Dans ce tableau sont présentées la variance résiduelle finale, la variation de variance due à la mise à l'échelle des configurations à la rotation et à la translation. Le calcul de la statistique F de Fisher permet de comparer les contributions relatives des différentes transformations. Les probabilités correspondantes permettent d'évaluer si les transformations ont un effet significatif ou non en termes de réduction de la variance.

Résidus

Résidus par objet : ce tableau et le diagramme en bâtons correspondant permettent de visualiser la répartition de la variance résiduelle par objet. On peut ainsi repérer pour quels objets la GPA a été moins efficace, autrement dit, quels objets se démarquent le plus de la configuration consensuelle. Résidus par configuration : ce tableau et le diagramme en bâtons correspondant permettent de visualiser la répartition de la variance résiduelle par configuration. On peut ainsi repérer pour quelles configurations l’analyse procrustéenne généralisée a été moins efficace, autrement dit, quelles configurations se démarquent le plus de la configuration consensuelle.

Facteurs de mise à l'échelle pour chaque configuration

Les facteurs de mise à l'échelle pour chaque configuration présentés dans un tableau et un diagramme permettent sont utilisés en analyse sensorielle pour comprendre comment les sujets ou experts utilisent différemment les échelles de notation.

Matrices de rotation : les matrices de rotation appliquées à chaque configuration sont affichées si l'utilisateur l'a demandé.

Résultats du test de consensus

Le nombre de permutations effectuées, la valeur Rc qui correspond à la proportion de variance totale expliquée par le consensus, et le quantile correspondant à Rc étant donnée la distribution de Rc obtenue suite aux permutations sont donnés pour évaluer si l’analyse procrustéenne généralisée est efficace. On fixe un intervalle de confiance (typiquement 95%), et si le quantile est au-delà de l'intervalle de confiance, on conclut que l’analyse procrustéenne généralisée a significativement réduit la variance.

Résultats du test de dimensions

Pour chaque facteur retenu à l'issue de l'ACP, le nombre de permutations effectuées, le F calculé suite à l’analyse procrustéenne généralisée (F est ici le rapport de la variance entre les objets sur la variance entre les configurations), le quantile correspondant au F étant donnée la distribution de F obtenue suite aux permutations sont donnés pour évaluer si un facteur contribue significativement à la qualité de l’analyse procrustéenne généralisée. On fixe un intervalle de confiance (typiquement 95%), et si le quantile est au-delà de l'intervalle de confiance, on conclut que le facteur contribue significativement. A titre indicatif sont aussi affichées les valeurs critiques et les p-values de la distribution F de Fisher pour le niveau alpha choisi. Il se peut que les conclusions issues de la distribution F de Fisher soit très différentes de ce qu'indique le test de permutation : l'utilisation de la distribution F de Fisher suppose la normalité des données, ce qui n'est pas nécessairement le cas.

Résultats pour la configuration consensus

• Coordonnées des objets avant l'ACP : ce tableau correspond aux coordonnées moyennes des objets, après les transformations de l’analyse procrustéenne généralisée, et avant l'ACP.
• Valeurs propres : si une ACP a été demandée, le tableau des valeurs propres et le diagramme en bâtons correspondant sont affichés. De ces valeurs propres est déduit le pourcentage de variabilité totale correspondant à chaque axe.
• Corrélations des variables avec les facteurs : ces résultats correspondent aux corrélations entre les variables de la configuration consensus avant les transformations, avec les facteurs obtenus après les transformations (analyse procrustéenne généralisée et ACP si cette dernière a été demandée).
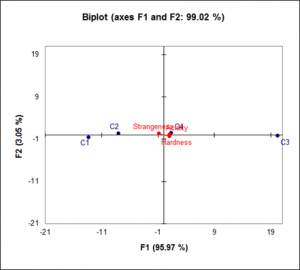
• Coordonnées des objets : ce tableau correspond aux coordonnées moyennes des objets, après les transformations de l’analyse procrustéenne généralisée puis de l'ACP si cette dernière a été demandée. Ces résultats sont utilisés pour la construction du graphique des objets.

Résultats pour les configurations après transformations

• Variance par configuration et par facteur : ce tableau, et le diagramme en bâtons qui lui correspond, permettent de visualiser comment se répartit pour chaque configuration la variance pour chacun des facteurs générés par l'ACP.
• Corrélations entre les variables et les facteurs : ces résultats correspondent aux corrélations entre les coordonnées des configurations avant et après les transformations (GPA et ACP si cette dernière a été demandée). Ces résultats sont utilisés pour construire le cercle des corrélations si une ACP a été effectuée. Sur le cercle des corrélations, les libellés explicites des variables utilisées pour chaque configuration sont affichés.
• Coordonnées des objets (présentation par configuration) : cette série de tableau correspond aux coordonnées des objets pour chaque configuration, après les transformations de l’analyse procrustéenne généralisée puis de l'ACP si cette dernière a été demandée. Ces résultats sont utilisés pour la construction de la première série de graphiques des objets.
• Coordonnées des objets (présentation par objet) : cette série de tableaux correspond aux coordonnées des objets pour chaque configuration, après les transformations de l’analyse procrustéenne généralisée puis de l'ACP si cette dernière a été demandée. Ces résultats sont utilisés pour la construction de la seconde série de graphiques des objets.