Analyse Canonique des Correspondances (ACC)

L'analyse canonique des correspondances (en anglais, Canonical Correspondence Analysis, ou CCA) a été développée dans le cadre d'applications en écologie (Ter Braak, 1986). Néanmoins, cette méthode dont le cadre conceptuel est bien défini, peut être utilisée dans d'autres domaines. Le géomarketing et les analyses démographiques devraient pouvoir en tirer profit.

Principe de l'analyse canonique des correspondances

Soit T1 un tableau de contingence correspondant au comptage en n sites des effectifs de p objets. Ce tableau peut être analysé avec une analyse factorielle des correspondances (AFC) afin d'obtenir une visualisation simultanée des sites et des objets en deux ou trois dimensions.

Soit T2 un tableau correspondant aux mesures en les mêmes n sites de q variables quantitatives et/ou qualitatives.

L'analyse canonique des correspondances permet d'analyser la relation entre T1 et T2, et d'obtenir une représentation simultanée des sites, des objets, et des variables en deux ou trois dimensions, optimale pour un critère de variance (Ter Braak 1986, Chessel 1987).

L'analyse canonique des correspondances peut être décomposée en deux parties :

1. une analyse sous contraintes dans un espace de dimension q. Cette partie est celle qui présente le plus d'intérêt car elle permet de relier l'analyse du tableau T1 à T2.
2. une analyse de la partie résiduelle, non contrainte, dans un espace de dimension min(n-1-q, p-1). Cette analyse est dénommée ACC non-contrainte.

Méthodes dérivées de l’analyse canonique des correspondances

Analyse canonique des correspondances partielle

L'analyse canonique des correspondances partielle ajoute une étape préliminaire. Le tableau T2 est subdivisé en deux groupes de variables : le premier contient des variables de conditionnement dont on veut supprimer l'effet, déjà connu ou sans intérêt pour l'étude, en réalisant une première analyse canonique des correspondances ; le second contient les variables dont on veut étudier l'effet. Une analyse canonique des correspondances est alors réalisée sur le tableau des résidus de la première analyse canonique des correspondances. L'analyse canonique des correspondances partielle permet donc d'étudier l'effet du second groupe de variables, sans que les variables du premier groupe ne viennent perturber l'analyse.

PLS-ACC

Tenenhaus (1998) a montré la possibilité d'utiliser la PLS dans le contexte de l'analyse canonique des correspondances. Addinsoft est le premier éditeur à proposer une intégration complète et efficace entre les deux méthodes. En utilisant une restructuration des données inspirée de la proposition de Tenenhaus, une étape PLS est appliquée aux données, soit pour créer des composantes PLS orthogonales optimales pour l'analyse canonique des correspondances qui permettent d'éviter les contraintes de l'analyse canonique des correspondances en termes de nombre de variables utilisables, soit pour sélectionner les variables les plus influentes avant de réaliser l'analyse canonique des correspondances. Les calculs de la seconde étape étant réalisés suivant la méthode classique d'analyse canonique des correspondances et les résultats habituels étant proposés, les utilisateurs coutumiers de l'analyse canonique des correspondances peuvent voir cette méthode comme une méthode de sélection de variables permettant de réduire le nombre de variables ou simplement de visualiser leur importance relative grâce au graphique des VIP. Dans le cas d'une analyse canonique des correspondances partielle, l'étape préliminaire est inchangée.

La terminologie Sites/Objets/Variables a été choisie dans XLSTAT. « Individus » ou « observations » pourraient être utilisés à la place de « sites », et « espèces » pourrait être utilisé à la place de « objets » dans le cadre d'une étude en écologie.

Résultats de l'analyse canonique des correspondances

• Inertie : dans ce tableau est affichée la répartition de l'inertie entre l'analyse canonique des correspondances contrainte et l'analyse canonique des correspondances non contrainte.
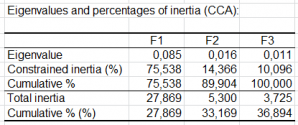
• Valeurs propres et pourcentages d'inertie : dans ces tableaux sont affichés pour l'analyse canonique des correspondances contrainte et l'analyse canonique des correspondances non contrainte, les valeurs propres, l'inertie associée, et les pourcentages correspondant, soit en terme d'inertie contrainte (ou non-contrainte), soit en terme d'inertie totale.
• Moyennes pondérées : dans ce tableau sont affichées les moyennes pondérées pour chacun des sites, ainsi que les moyennes pondérées globales.
• Pour l'ensemble des sites, objets et variables sont ensuite affichées les coordonnées principales, les coordonnées standards. Ces coordonnées sont utilisées pour les différents graphiques générés ensuite.
• Coefficients de régression : dans ce tableau sont affichés les coefficients de régression des variables sur les axes factoriels.
• Les graphiques permettent de visualiser la relation entre les sites, les objets et les variables. Lorsque des variables qualitatives ont été utilisées, les modalités correspondantes apparaissent en rouge avec un cercle évidé sur les graphiques. La légende les présente comme « modalités » afin de les différencier des autres variables explicatives.