Tests de normalité

Pourquoi faire un test de Normalité ?

Supposer la normalité d'un échantillon ou d'une statistique est commun en statistique. Pourtant, la vérification de l'hypothèse de normalité est souvent négligée. Par exemple, la normalité des résidus obtenus lors d'une régression linéaire est rarement testée, alors qu'elle conditionne la qualité des intervalles de confiance autour des paramètres et des prédictions.

Tests de Normalité dans XLSTAT

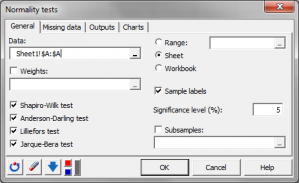
XLSTAT propose quatre tests pour tester la normalité d'un échantillon :

• le test de Shapiro-Wilk bien adapté aux échantillons de moins de 5000 observations ;
• le test d'Anderson-Darling est une modification du test de Kolmogorov-Smirnov adaptée à plusieurs lois dont la loi normale, pour le cas où les paramètres de la loi ne sont pas connus et doivent donc être estimés ;
• le test de Lilliefors est une modifiication du test de Kolmogorov-Smirnov adapté au cas de la normalité dans le cas où les paramètres de la loi, la moyenne et la variance, ne sont pas connus et doivent donc être estimés ;
• le test de Jarque-Bera qui est d'autant plus performant que le nombre de données est important.

Graphiques pour représenter la Normalité des échantillons

Afin de vérifier visuellement si un échantillon suit une loi normale, il est possible d'utiliser les graphiques P-P et les graphiques Q-Q :

• Graphiques P-P (loi normale) : les graphiques Probabilité-Probabilité (P-P plots en anglais) permettent de comparer la fonction de répartition empirique d'un échantillon à celle d'un échantillon distribué suivant une loi normale de même moyenne et même variance. Si l'échantillon suit une loi normale, les points doivent être confondus avec la première bissectrice du plan.
• Graphiques Q-Q (loi normale) : les graphiques Quantile-Quantile (Q-Q plots en anglais) permettent de comparer les quantiles de l'échantillon à ceux d'un échantillon distribué suivant une loi normale de même moyenne et même variance. Si l'échantillon suit une loi normale, les points doivent être confondus avec la première bissectrice du plan.

Cet outil complète l' « ajustement à une loi de probabilité », outil qui vous permet de déterminer la valeur des paramètres de la distribution normale et de tester la qualité de l'ajustement en utilisant un Chi-carré ou un test de Kolmogorov Smirnov.