Histogrammes

Les histogrammes sont un outil très courant pour évaluer la forme de la distribution d'une série de valeurs. Ils sont disponibles en format Excel grâce au logiciel statistique XLSTAT.

Qu’est ce qu’un histogramme ?

L'histogramme est l'un des outils de visualisation les plus utilisés car il permet d'avoir très rapidement une idée de la distribution d'un échantillon de données quantitatives continues ou discrètes.

Options pour la représentation des histogrammes dans XLSTAT

XLSTAT propose plusieurs options pour obtenir l'histogramme le mieux adapté à vos données :

Définition des intervalles L'un des enjeux pour la création d'un histogramme est la définition des intervalles, car pour un jeu de données déterminé, l'allure de l'histogramme en dépend entièrement. Entre les deux extrêmes de l'intervalle unique comprenant toutes les données et donnant une seule barre, et de l'histogramme où il y a un intervalle par donnée, il existe autant d'histogrammes possibles que de partitions des données. Afin de faciliter l'obtention d'histogrammes, XLSTAT vous propose de créer vos histogrammes :
- soit en définissant le nombre d'intervalles,
- soit en définissant leur amplitude,
- soit en spécifiant vous-même les intervalles.
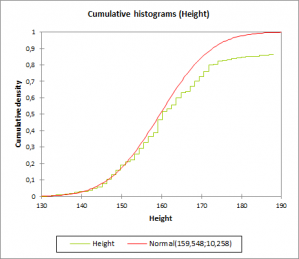
Histogramme cumulé XLSTAT vous permet de créer des histogrammes cumulés qui correspondent soit au cumul des valeurs de l'histogramme, soit à la fonction de répartition empirique. L'utilisation de la fonction de répartition empirique est recommandée pour une comparaison à une fonction de répartition d'une distribution théorique.
Comparaison à une distribution théorique XLSTAT vous permet de comparer, si vous le souhaitez, l'histogramme à une distribution théorique dont vous pouvez fixer les paramètres. Néanmoins, si vous souhaitez vérifier si un échantillon est distribué suivant une loi donnée, vous pouvez utiliser l'outil d'ajustement d'une loi de distribution pour estimer les paramètres de la loi et éventuellement vérifier si l'hypothèse est acceptable.