Graphiques univariés

Pourquoi utiliser des graphiques univariés ?

Avant d'utiliser des méthodes d'analyse avancées comme par exemple une analyse discriminante ou une régression multiple, il est nécessaire dans un premier temps, de découvrir les données afin d'identifier des tendances, de repérer des anomalies ou tout simplement de disposer d'informations essentielles telles que le minimum, le maximum, ou la moyenne d'un échantillon de données.

XLSTAT vous propose un nombre important de statistiques descriptives et de graphiques qui vous permettront d'avoir un premier aperçu pertinent de vos données.

Bien que vous puissiez sélectionner plusieurs variables (ou échantillons) à la fois, XLSTAT calcul l'ensemble des statistiques descriptives pour chacun des échantillons indépendamment.

Graphiques pour les données quantitatives

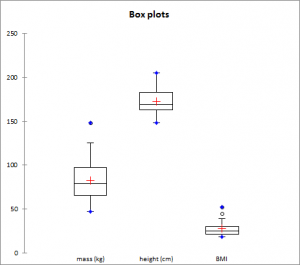
• Box plots ces représentations univariées d'échantillons de données quantitatives sont parfois appelées « diagrammes boîtes et moustaches ». C'est une représentation simple et assez complète puisque dans la version proposée par XLSTAT sont affichés le minimum, le 1er quartile, la médiane, la moyenne, le 3ième quartile, ainsi que les deux limites (les extrémités des « moustaches ») au-delà desquelles on peut considérer que les valeurs sont anormales.
• Scattergrams ces représentations univariées permettent de donner une idée de la distribution et de la pluralité éventuelle des modes d'un échantillon. Tous les points sont représentés, ainsi que la moyenne et la médiane.
• Strip plots ces diagrammes représentent sous forme de bandes (strip en anglais) les données de l'échantillon. Sur un intervalle donné, plus les bandes sont serrées ou épaisses plus il y a de données.
• Graphiques P-P (loi normale) les graphiques Probabilité-Probabilité (P-P plots en anglais) permettent de comparer la fonction de répartition empirique d'un échantillon à celle d'un échantillon distribué suivant une loi normale de même moyenne et même variance. Si l'échantillon suit une loi normale, les points doivent être confondus avec la première bissectrice du plan.
• Graphiques Q-Q (loi normale) les graphiques Quantile-Quantile (Q-Q plots en anglais) permettent de comparer les quantiles de l'échantillon à ceux d'un échantillon distribué suivant une loi normale de même moyenne et même variance. Si l'échantillon suit une loi normale, les points doivent être confondus avec la première bissectrice du plan.

Graphiques pour les données qualitatives

• Diagrammes en bâtons activez cette option pour représenter sous forme de diagrammes en bâtons les effectifs ou les fréquences des différentes modalités des variables qualitatives.
• Diagrammes en secteurs activez cette option pour représenter sous forme de diagrammes en secteurs (ou camemberts) les effectifs ou les fréquences des différentes modalités des variables qualitatives.
• Diagrammes en secteurs doubles ces graphiques permettent de comparer les effectifs ou les fréquences de sous-échantillons à ceux d'un échantillon complet.
• Anneaux cette option n'est active que si une colonne de sous-échantillons a été sélectionnée. Ces graphiques permettent de comparer les effectifs ou les fréquences des sous-échantillons à ceux d'un échantillon complet.
• Barres empilées cette option n'est active que si une colonne de sous-échantillons a été sélectionnée. Ces graphiques permettent de comparer les effectifs ou les fréquences des sous-échantillons à ceux d'un échantillon complet.