Modèles mixtes

Principes des modèles mixtes

Les modèles mixtes sont des modèles complexes qui ont été développés à partir du modèle linéaire. Ils permettent de prendre en compte, d'une part, la notion de mesure répétée et, d'autre part, celle de facteur aléatoire. Les variables explicatives pourront être aussi bien quantitatives que qualitatives. XLSTAT permet aussi de faire une ANOVA sur mesures répétées en utilisant les modèles mixtes.

L'équation du modèle aura donc la forme suivante :

y = Xβ + Zγ + ε

où y est la variable quantitative à expliquer, X rassemble les facteurs associés aux effets fixes (ce sont les variables classiques de la régression linéaire), β est un vecteur de coefficients associés aux effets fixes, Z est une matrice rassemblant les effets aléatoires (ce sont des variables qui ne peuvent pas être supposées fixes), γ est un vecteur de coefficients associés aux effets aléatoire et ε est un vecteur rassemblant les erreurs associées à chaque observation.

L’estimation des paramètres du modèle se fait grâce à l’estimateur du maximum de vraisemblance. Les modèles mixtes permettent de spécifier des matrices de covariance spécifiques entre les variables.

En outre, les interactions utilisées dans le modèle peuvent facilement être défini dans XLSTAT.

XLSTAT permet le calcul des tests de type I, II et III des effets fixes. Le principe de ces tests est le même que dans le cas du modèle linéaire. Néanmoins, leur calcul est légèrement différent.

Options de calculs pour les modèles mixtes dans XLSTAT

Comme dans l’ANOVA classique, en ANOVA à mesures répétées, des comparaisons multiples peuvent être effectuées. Cela sert à vérifier si les catégories d'un facteur sont différentes ou non. De nombreux tests ont été proposés pour comparer les moyennes des catégories.

La majorité de ces tests supposent que l'échantillon est normalement distribué. XLSTAT fournit les principaux tests. Dans le cas d’ANOVA à mesures répétées, les écarts-types sont obtenus en utilisant les estimations du maximum de vraisemblance.

Résultats pour les modèles mixtes

Matrice de corrélation : ce tableau est affiché afin de vous permettre d'avoir un aperçu des corrélations entre les différentes variables sélectionnées.
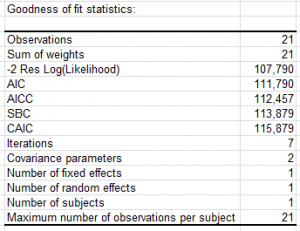
Coefficients d'ajustement : dans ce tableau sont affichées les statistiques relatives à l'ajustement du modèle de régression :
- Observations : le nombre d'observations prises en compte dans les calculs. Dans les formules présentées ci-dessous n désigne le nombre d'observations.
- Somme des poids : la somme des poids des observations prises en compte dans les calculs. Dans les formules présentées ci-dessous W désigne la somme des poids.
- AIC : le critère d'information d'Akaike (Akaike's Information Criterion). Ce critère proposé par Akaike (1973) dérive de la théorie de l'information, et s'appuie sur la mesure de Kullback et Leibler (1951). C'est un critère de sélection de modèles qui pénalise les modèles pour lesquels l'ajout de nouvelles variables explicatives n'apporte pas suffisamment d'information au modèle. On cherche à minimiser le critère AIC.
- AICC : ce critère (Hurvich et Tsai, 1989) est issu de l'AIC.
- SBC : le critère Bayésien de Schwarz (Schwarz's Bayesian Criterion) . Ce critère proposé par Schwarz (1978) est proche du critère AIC, et comme ce dernier on cherche à le minimiser. Il est aussi appelé BIC.
- CAIC : ce critère (Bodzogan, 1987).
- Itérations : nombre d'itérations nécessaires à la convergence de l'algorithme de Newton-Raphson.
- Paramètres de covariance : nombre de paramètres à estimer dans la matrice V.
- Nombre d'effets fixes.
- Nombre d'effets aléatoires.
Paramètres de covariance – Facteur répété : dans ce tableau sont affichés les paramètres associés à la matrice de covariance des erreurs R. Pour chaque paramètre, l'écart type, la valeur de la statistique Z ainsi que la p-valeur associée sont obtenus.
Paramètres de covariance – Facteur aléatoire (uniquement pour les modèles mixtes): dans ce tableau sont affichés les paramètres associés à la matrice de covariance des coefficients des effets aléatoires G. Pour chaque paramètre, l'écart type, la valeur de la statistique Z ainsi que la p-valeur associée sont obtenus.
Test du rapport de vraisemblance : dans ce tableau sont affichés les résultats du test de comparaison des vraisemblances associées, d'une part, au modèle sans variables explicatives et, d'autre part, au modèle sélectionné. Le rapport de vraisemblance, la statistique du chi² ainsi que la p-valeur sont affichés.
Paramètres du modèle : ce tableau rassemble les coefficients associés aux effets fixes du modèle. Pour chaque variable, l'écart-type, la statistique t, la p-valeur, ainsi que l'intervalle de confiance sont calculés.
Coefficients des effets aléatoires (uniquement pour les modèles mixtes): ce tableau rassemble les coefficients associés aux effets aléatoires du modèle. Pour chaque variable, l'écart-type, le nombre de degrés de liberté, la statistique t, la p-valeur, ainsi que l'intervalle de confiance sont calculés.
Le tableau des tests de type I des effets fixes permet de visualiser l'influence de l'ajout progressif des variables explicatives sur l'ajustement du modèle, au sens du F de Fisher, ou de la probabilité associée au F de Fisher. Plus la probabilité est faible, plus la contribution de la variable au modèle est importante, toutes les autres variables étant déjà dans le modèle. Remarque : l'ordre de sélection des variables dans le modèle influe sur les valeurs obtenues.
Le tableau des tests de type III des effets fixes permet de visualiser l'influence du retrait d'une variable explicative sur l'ajustement du modèle, toutes les autres variables étant conservées, au sens du F de Fisher, ou de la probabilité associée au F de Fisher. Plus la probabilité est faible, plus la contribution de la variable au modèle est importante, toutes les autres variables étant déjà dans le modèle.
Dans le tableau des prédictions et résidus sont donnés pour chaque observation, son poids, la valeur de la variable dépendante, la prédiction du modèle, les intervalles de confiance, ainsi que les résidus. Plusieurs types de résidus sont affichés :
- les résidus bruts : r_i = y_i - x_iβ
- les résidus studentisés : r_i^stud = r_i / √var(r_i)
- les résidus de Pearson : r_i^pearson = r_i / √var(y_i)
- les résidus conditionnels : r_i^cond = r_i - z_i’ γ
- les résidus conditionnels studentisés : r_i^{cond / stud} = r_i^cond / √var(r_i^cond)
- les résidus conditionnels de Pearson : r_i^{cond / stud} = r_i^cond / √var(y_i)