Régression sur les Composantes Principales (PCR)
La régression en composantes principales (PCR) combine les méthodes PCA et OLS. Disponible dans Excel avec le logiciel XLSTAT.
Principes de la régression sur les composantes principales
La régression sur les composantes principales ou PCR (Principal Components Regression) comprend trois étapes :
- on réalise d'abord une ACP (Analyse en Composantes Principales) sur le tableau des variables explicatives,
- puis on effectue une régression OLS aussi appelée régression linéaire sur les composantes retenues,
- enfin on calcule les paramètres du modèle sur les variables d'origine.
Equations du modèle de la régression sur les composantes principales
L'ACP permet de passer d'un tableau X comprenant n observations décrites par p variables à un tableau S de n observations décrites par q composantes, où q est inférieur ou égal à p et tel que (S'S) est inversible. Une sélection supplémentaire peut être effectuée de telle sorte que seuls les r composantes les plus corrélées avec la variable Y soient gardées pour la régression OLS. On obtient alors le tableau R.
Le calcul de la régression OLS s'effectue sur le tableau R. On obtient alors les paramètres correspondant à chacun des r facteurs. Afin de palier le problème d'interprétation des paramètres ainsi obtenus, XLSTAT effectue automatiquement les calculs nécessaires pour obtenir les paramètres et les intervalles de confiance pour les variables de départ.
Résultats graphiques de la régression sur les composantes principales : Graphiques des corrélations, des individus et biplots
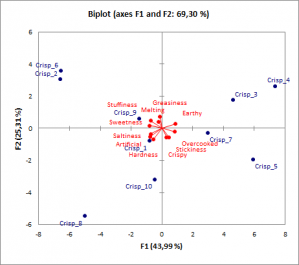
Grâce à la première étape, analyse en composantes principales, la régression PCR a l'avantage sur la régression classique de proposer des graphiques facilement interprétables. Ceux-ci représentent les relations entre les variables explicatives entre elles, ainsi qu'avec la variable dépendante. Le graphique des individus ou score plot permet quant à lui d'étudier les proximités entre les échantillons et la structure du jeu de données. Le bi-plot réunit ces trois types d'information.
Prédiction grâce à la régression sur les composantes principales
La régression en composantes principales (PCR) est aussi utilisée a des fins prédictives. XLSTAT permet de prédire de nouveaux résultats avec une erreur estimée connue.
Dans le tableau des prédictions et résidus sont donnés pour chaque observation, son poids, la valeur de la variable explicative qualitative s'il n'y en a qu'une, la valeur observée de la variable dépendante, la prédiction du modèle, les résidus, les intervalles de confiance, ainsi que la prédiction ajustée. Deux types d'intervalles de confiance sont affichés : un intervalle de confiance autour de la moyenne et un intervalle autour de la prédiction ponctuelle.
Options pour la régression PCR dans XLSTAT
ACP normée : activez cette option pour effectuer une ACP sur la matrice de corrélation. Désactivez cette option pour effectuer une ACP sur la matrice de covariance.
Filtrer les composantes : vous pouvez activer l'une ou les deux options suivantes afin de réduire le nombre de composantes utilisées dans le modèle :
% minimum : activez cette option puis saisissez le pourcentage minimum de la variabilité totale que doivent représenter les composantes sélectionnées.
Nombre maximum : activez cette option pour fixer le nombre maximum de composantes à prendre en compte.
Trier les composantes : choisissez l'une des options suivantes afin de déterminer quel critère est utilisé pour trier les composantes avant que soient pris en compte les critères « % minimum » ou « Nombre maximum »:
Corrélations avec les Y : activez cette option pour que la sélection des composantes se fasse après un tri décroissant suivant le carré du coefficient de corrélation (R²) entre la variable Y et les composantes. Cette option est recommandée.
Valeurs propres : activez cette option pour que la sélection des composantes se fasse après un tri décroissant suivant les valeurs propres associées aux composantes.


analysez vos données avec xlstat
Fonctionnalités corollaires