ANOVA sur mesures répétées

Principes de l'analyse de variance sur mesures répétées

L'analyse de variance sur mesures répétées utilise le même cadre conceptuel que l'analyse de la variance classique. Les variables explicatives sont qualitatives et la variable dépendante est quantitative et est mesurée plusieurs fois. Chacune de ces mesures est appelée répétition. Dans le cadre de l'ANOVA à mesures répétées, les variables explicatives sont souvent appelées facteurs.

Si p est le nombre de facteurs, le modèle de l'ANOVA au temps t s'écrit de la manière suivante :

y^t_i = β₀ + ∑_j=1...p β_{k_(i,j),j} + ε_i

où y^t_i est la valeur observée pour la variable dépendante pour l'observation i au temps t, k_(i,j) est l'indice correspondant à la modalité du facteur j pour l'observation i, et ε_i est l'erreur du modèle.

Les hypothèses utilisées en ANOVA à mesures répétées sont identiques à celles de la régression linéaire : les erreurs ε_i suivent une même loi normale N(0,s) et sont indépendantes.

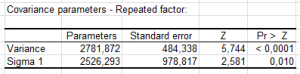
Néanmoins, certaines hypothèses supplémentaires sont nécessaires. Comme les différentes répétitions sont effectuées sur les mêmes individus, on ne pourra pas supposer que y^t₁ et y^t₂ sont indépendantes, on supposera néanmoins que la matrice de covariance entre les y est sphérique. Cette hypothèse peut être relâchée lorsqu'on utilise les modèles mixtes.

Le principe de l'ANOVA sur mesures répétées est simple, on va effectuer T ANOVA classique sur chaque répétition t₁,…, t_T et ensuite on va tester la sphéricité de la matrice de covariance entre les répétitions en utilisant le test de Mauchly et les epsilons de Greenhouse-Geisser et Huynt-Feldt. Si l'hypothèse de sphéricité est vérifiée, on pourra analyser les tests sur les effets intra- et inter-sujets.

Interactions pour l'analyse de variance sur mesures répétées

On désigne par interaction un facteur artificiel (non mesuré) reflétant l'interaction entre au moins deux facteurs mesurés. Par exemple, si on applique un traitement à une plante, et que les essais sont réalisés sous deux intensités lumineuses différentes, on pourra inclure dans le modèle un facteur d'interaction traitement*lumière qui permettra d'identifier une éventuelle interaction entre les deux facteurs. S'il y a une interaction entre les deux facteurs, on observera sur les plantes un effet significativement plus important lorsque la lumière est forte et que le traitement est de type 2, alors que l'effet est moyen pour les couples (lumière faible, traitement 2) et (lumière forte, traitement 1).

Pour faire un parallèle avec la régression linéaire, les interactions sont équivalentes à des produits entre les valeurs explicatives continues, bien qu'ici l'obtention des interactions nécessite plus qu'une simple multiplication entre deux variables. Néanmoins la notation utilisée pour représenter l'interaction entre le facteur A et le facteur B est A*B.

XLSTAT permet de facilement définir les interactions à prendre en compte dans le modèle.

Facteurs imbriqués pour l'analyse de variance sur mesures répétées

Lorsqu'on ne peut pas croiser toutes les modalités de deux facteurs, alors on peut utiliser des facteurs imbriqués ou hiérarchiques. Par exemple, si l'on cherche à analyser le lien entre certaines caractéristiques d'un produit en sortie d'une chaîne de fabrication et les opérateurs et les machines impliqués, et si les opérateurs travaillent sur une machine donnée avec par exemple quatre opérateurs en rotation, alors chaque opérateur n'est pas croisé avec chaque machine, mais est associé à une seule machine. On a alors un effet imbriqué (l'effet opérateur est imbriqué dans l'effet machine).

XLSTAT permet d'identifier automatiquement les facteurs imbriqués. Par ailleurs, il est possible d'inclure dans le modèle un facteur imbriqué.

Contraintes pour l'analyse de variance sur mesures répétées

Au cours des calculs, chaque facteur est décomposé en une sous-matrice contenant autant de colonnes qu'il y a de modalités dans le facteur. Typiquement, il s'agit d'un tableau disjonctif complet. Cette décomposition pose néanmoins un problème : s'il y a g modalités, le rang de cette sous-matrice n'est pas g mais g-1. Cela entraîne la nécessité de supprimer l'une des colonnes de la sous-matrice, et éventuellement de transformer les autres colonnes. Plusieurs stratégies sont possibles en fonction de l'interprétation que l'on veut ensuite faire :

a1=0 : le paramètre correspondant à la première modalité est nul. Ce choix permet d'imposer que l'effet de la première modalité correspond à un standard. Dans ce cas, la constante du modèle est égale à la moyenne de la variable dépendante pour le groupe 1.
an=0 : le paramètre correspondant à la dernière modalité est nul. Ce choix permet d'imposer que l'effet de la dernière modalité correspond à un standard. Dans ce cas, la constante du modèle est égale à la moyenne de la variable dépendante pour le groupe g.

Remarque : si le choix de la contrainte influence la valeur des paramètres, il n'en a aucun sur les valeurs prédites et sur les différentes statistiques d'ajustement.

Tests de comparaisons multiples pour l'analyse de variance sur mesures répétées

L'une des applications principales de l'ANOVA sont les tests de comparaisons multiples dont le but est de vérifier si les paramètres correspondant aux différentes modalités d'un facteur sont significativement différents ou non. Par exemple, dans le cas où quatre traitements sont appliqués à des plantes, on veut savoir non seulement si les traitements ont un effet significatif, mais aussi si les traitements ont un effet différent.

De nombreux tests ont été proposés pour comparer les moyennes des modalités. La majorité de ces tests s'appuie aussi sur l'hypothèse de normalité. XLSTAT propose les principaux tests parmi lesquels : XLSTAT propose les principaux tests pour comparer les moyennes des modalités, parmi lesquels :

Test de Tukey HSD,
Test du t de Bonferroni,
Test de Dunn-Sidak,
Test de Newman-Keuls (SNK),
Test de Duncant,
Test REGWQ.

Résultats pour l’analyse de la variance sur mesures répétées

Coefficients d'ajustement : dans ce tableau sont affichées les statistiques relatives à l'ajustement du modèle de régression :
- Observations : le nombre d'observations prises en compte dans les calculs. Dans les formules présentées ci-dessous n désigne le nombre d'observations.
- Somme des poids : la somme des poids des observations prises en compte dans les calculs. Dans les formules présentées ci-dessous W désigne la somme des poids.
- DDL : le nombre de degrés de liberté pour le modèle retenu (correspondant à la partie erreurs).
- R² : le coefficient de détermination du modèle. Le R² s'interprète comme la proportion de la variabilité de la variable dépendante expliquée par le modèle. Plus le R² est proche de 1, meilleur est le modèle. L'inconvénient du R² est qu'il ne prend pas en compte le nombre de variables utilisées pour ajuster le modèle.
- R² ajusté : le coefficient de détermination ajusté du modèle. Le R² ajusté peut être négatif si le R² est voisin de zéro. Ce coefficient n'est affiché que si la constante du modèle n'est pas fixée par l'utilisateur. Le R² ajusté est une correction du R² qui permet de prendre en compte le nombre de variables utilisées dans le modèle.
- MCE : la moyenne des carrés des erreurs (MCE) est définie par :
- RMCE : la racine de la moyenne des carrés des erreurs (RMCE) est la racine carrée de la MCE.
- MAPE : la Mean Absolute Percentage Error
- DW : le coefficient de Durbin-Watson. Ce coefficient correspond au coefficient d'autocorrélation d'ordre 1 et permet de vérifier que les résidus du modèle ne sont pas autocorrélés, sachant que l'indépendance des résidus est l'une des hypothèses de base de la régression linéaire. L'utilisateur pourra se référer à une table des coefficients de Durbin-Watson pour vérifier si l'hypothèse d'indépendance des résidus est acceptable.
- Cp : le coefficient Cp de Mallows .
- AIC : le critère d'information d'Akaike (Akaike's Information Criterion). Ce critère proposé par Akaike (1973) dérive de la théorie de l'information, et s'appuie sur la mesure de Kullback et Leibler (1951). C'est un critère de sélection de modèles qui pénalise les modèles pour lesquels l'ajout de nouvelles variables explicatives n'apporte pas suffisamment d'information au modèle, l'information étant mesurée au travers de la SCE. On cherche à minimiser le critère AIC.
- SBC : le critère bayésien de Schwarz (Schwarz's Bayesian Criterion). Ce critère proposé par Schwarz (1978) est proche du critère AIC, et comme ce dernier on cherche à le minimiser.
- PC : le critère de prédiction d'Amemiya (Amemiya's Prediction Criterion). Ce critère proposé par Amemiya (1980) permet comme le R² ajusté de tenir compte de la parcimonie du modèle.
Le tableau d'analyse de la variance permet d'évaluer le pouvoir explicatif des variables explicatives. Dans le cas où la constante du modèle n'est pas fixée à une valeur donnée, le pouvoir explicatif est évalué en comparant l'ajustement (au sens des moindres carrés) du modèle final avec l'ajustement du modèle rudimentaire composé d'une constante égale à la moyenne de la variable dépendante. Dans le cas où la constante du modèle est fixée, la comparaison est faite par rapport au modèle pour lequel la variable dépendante serait égale à la constante fixée.
Le tableau des Type I SS permet de visualiser l'influence de l'ajout progressif des variables explicatives sur l'ajustement du modèle, au sens de la somme des carrés des erreurs (SCE), de la moyenne des carrés des erreurs (MCE), du F de Fisher, ou de la probabilité associée au F de Fisher. Plus la probabilité est faible, plus la contribution de la variable au modèle est importante, toutes les autres variables étant déjà dans le modèle. Remarque : l'ordre de sélection des variables dans le modèle influe sur les valeurs obtenues.
Le tableau des Type III SS permet de visualiser l'influence du retrait d'une variable explicative sur l'ajustement du modèle, toutes les autres variables étant conservées, au sens de la somme des carrés des erreurs (SCE), de la moyenne des carrés des erreurs (MCE), du F de Fisher, ou de la probabilité associée au F de Fisher. Plus la probabilité est faible, plus la contribution de la variable au modèle est importante, toutes les autres variables étant déjà dans le modèle. Remarque : contrairement au cas des Type I SS, l'ordre de sélection des variables dans le modèle n'influe pas sur les valeurs obtenues, et contrairement aux Type II SS, les valeurs ne dépendent pas des effectifs des cellules (par cellule on entend une combinaison de modalités des différents facteurs), ce qui fait des Type III le test recommandé pour évaluer la contribution d'une variable.
Le tableau des coefficients normalisés (aussi appelés coefficients bêta) permet de comparer le poids relatif des variables. Plus la valeur absolue d'un coefficient est élevée, plus le poids de la variable correspondante est important. Lorsque l'intervalle de confiance autour des coefficients normalisés comprend la valeur 0 (cela est facilement visible sur le graphique des coefficients normalisés), le poids d'une variable dans le modèle n'est pas significatif.
Dans le tableau des prédictions et résidus sont donnés pour chaque observation, son poids, la valeur de la variable explicative qualitative s'il n'y en a qu'une, la valeur observée de la variable dépendante, la prédiction du modèle, les résidus, les intervalles de confiance. Deux types d'intervalles de confiance sont affichés : un intervalle de confiance autour de la moyenne (correspondant au cas où l'on ferait la prédiction pour un nombre infini d'observations avec un ensemble de valeurs données des variables explicatives) et un intervalle autour de la prédiction ponctuelle (correspondant au cas d'une prédiction isolée pour des valeurs données des variables explicatives). Le second intervalle est toujours plus grand que le premier, les aléas étant plus importants. Si des données de validation ont été sélectionnées, elles sont affichées en fin de tableau.

Si des tests de comparaison multiples ont été demandés, les résultats correspondant sont ensuite affichés. Finalement, les tableaux associés aux mesures répétées sont présentées :

Le test de sphéricité de Mauchly permet de valider l'hypothèse de sphéricité. La puissance de ce test est assez faible et il pourra poser des problèmes pour de petits échantillons. Dans ce tableau, on trouve aussi l'epsilon de Greenhouse-Geisser et l'epsilon de Huynt-Feldt. Ces deux statistiques permettent aussi de tester l'hypothèse de sphéricité. Plus elles sont proches de 1, plus on se rapprochera d'une matrice de covariance sphérique.
Test sur les effets intra-sujets : Ce tableau nous permet de voir quels facteurs ont un effet qui évolue d'une répétition à une autre.
Test sur les effets inter-sujets : Ce tableau nous permet de voir quels facteurs ont un effet qui diffère d'un sujet à un autre et non d'une répétition à une autre.

Résultats graphiques de l’analyse de la variance sur mesures répétées

Les graphiques qui suivent permettent de visualiser les résultats mentionnés ci-dessus. S'il n'y a qu'une seule variable explicative dans le modèle, le premier graphique affiché permet de visualiser les valeurs observées, la droite de régression et les deux types d'intervalles de confiance autour des prévisions. Le second graphique permet quant à lui de visualiser les résidus normalisés en fonction de la variable explicative. En principe, les résidus doivent être distribués de manière aléatoire autour de l'axe des abscisses. L'observation d'une tendance ou d'une forme révèlerait un problème au niveau du modèle.

Les trois graphiques affichés ensuite permettent de visualiser respectivement l'évolution des résidus normalisés en fonction de la variable dépendante, la distance entre les prédictions et les observations (pour un modèle idéal, les points seraient tous sur la bissectrice), et les résidus normalisés sur la forme d'un diagramme en bâtons. Ce dernier graphique permet de rapidement voir si un nombre anormal de données sort de l'intervalle ]-2, 2[ sachant que ce dernier, sous hypothèse de normalité, doit contenir environ 95% des données.

Voir tous les tutoriels