Tests t et z pour deux échantillons

Principe du test T de Student ou test Z

L'utilisation des tests paramétriques t et z permet de comparer les moyennes de deux échantillons. La méthode de calcul est différente en fonction de la nature des échantillons. On distingue le cas où les échantillons sont indépendants (par exemple, dans le cas d'une comparaison du chiffre d'affaires annuel par magasin entre deux régions pour une chaîne de supermarchés), du cas où ils sont appariés (par exemple, dans le cas d'une comparaison, à l'intérieur d'une même région, des chiffres d'affaires annuels entre deux années).

Les tests t et z sont dits paramétriques car ils supposent que les échantillons sont distribués suivant des lois normales. Cette hypothèse pourra être testée à l'aide des tests de normalité.

Comparaison des moyennes de deux échantillons indépendants

Soit un échantillon E1, comprenant n1 observations, de moyenne µ1 et de variance s1². Soit un second échantillon E2 indépendant de E1, comprenant n2 observations, de moyenne µ2 et de variance s2². Soit D la différence supposée entre les moyennes (D vaut 0 lorsque l'on suppose l'égalité).

On utilise :

• le test t de Student si on ne connaît pas la vraie variance des populations dont sont extraits les échantillons ;
• le test z si on connaît la vraie variance σ² de la population.

Test t de Student

L'utilisation du test t de Student nécessite de décider préalablement si les variances des échantillons doivent être considérées comme étant égales ou non. XLSTAT propose d'utiliser un test F de Fisher afin de tester l'hypothèse d'égalité des variances, et de tenir compte du résultat du test pour la suite des calculs.

Si l'on considère que les deux échantillons ont la même variance, on estime la variance commune par :

s² = [(n1-1)s1² + (n2-1)s2²] / (n1 + n2 - 2)

La statistique du test est alors donnée par :

t = (µ1 - µ2 -D) / (s √1/n1 + 1/n2)

La statistique t suit une loi de Student à n1+n2-2 degrés de liberté.

Si l'on considère que les variances sont différentes la statistique est donnée par :

t = (µ1 - µ2 -D) / (√s1²/n1 + s2²/n2)

Test z

Pour le test z, la variance s² de la population est supposée connue. L'utilisateur peut saisir cette valeur ou l'estimer à partir des données (ce dernier cas étant proposé uniquement à titre pédagogique). La statistique du test est donnée par :

z = (µ1 - µ2 -D) / (σ √1/n1 + 1/n2)

La statistique z suit une loi normale.

Comparaison des moyennes de deux échantillons appariés

Si deux échantillons sont appariés, ils sont nécessairement de même taille.

Dans le cas où des valeurs seraient manquantes pour certaines observations, soit on supprime l'observation des deux échantillons, soit on estime les valeurs manquantes.

On étudie la moyenne des différences calculées pour les n observations. Si d est la moyenne des différences, s² la variance des différences, et D la différence supposée, la statistique du test t est donnée par :

T= (d-D) ⁄ (s/√n)

La statistique t suit une loi de Student à n-1 degrés de liberté.

Pour le test z, la statistique, si σ² est la variance :

z= (d-D) ⁄ (σ/√n)

La statistique z suit une loi normale.

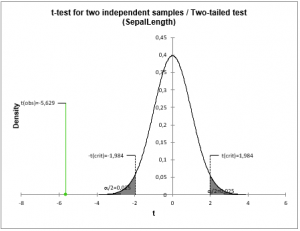
Hypothèses alternatives

Trois types de tests sont possibles en fonction de l'hypothèse alternative choisie :

• le test bilatéral :
  • H0 : µ1 = µ2
  • Ha : µ1 ≠ µ2
• le test unilatéral à gauche
  • H0 : µ1 = µ2
  • Ha : µ1 < µ2
• le test unilatéral à droite
  • H0 : µ1 = µ2
  • Ha : µ1 > µ2