Tests multidimensionnels (Mahalanobis, …)

Principes des tests multidimensionnels

Les tests mis en œuvre dans cet outil permettent de comparer des échantillons décrits par plusieurs variables. Par exemple, au lieu de comparer les moyennes de deux échantillons comme avec le test de Student, on compare ici simultanément pour les mêmes échantillons plusieurs moyennes mesurées pour différentes variables.

Par rapport à une procédure qui consisterait à faire autant de tests de Student qu’il y a de variables, la méthode proposée ici présente l’avantage d’utiliser la structure de covariance entre les variables et d’obtenir une conclusion globale. Il se peut que deux échantillons diffèrent pour une variable avec un test de Student, mais qu’au global on ne puisse rejeter l’idée qu’ils sont finalement semblables.

Distance de Mahalanobis

La distance de Mahalanobis permet de calculer la distance entre deux points dans un espace à p dimensions, en tenant compte de la structure de variance-covariance sur ces p dimensions. Le carré de cette distance se définit par :

dM² = (x1 - x2) ∑-1 (x1 - x2)

Autrement dit, c'est le produit de la transposée du vecteur des différences de coordonnées pour les p dimensions entre les deux points, multiplié par l'inverse de la matrice de covariance, multiplié par le vecteur des différences. La distance euclidienne, correspond à la distance de Mahalanobis dans le cas où la matrice de covariance est la matrice identité, c'est-à-dire que les variables sont centrées réduites et indépendantes.

La distance de Mahalanobis peut être utilisée pour comparer deux groupes car la statistique du T² de Hotelling définie par :

T² = [(n1*n2) ⁄ (n1 + n2)] dM

suit une loi de Hotelling, à condition que les échantillons suivent une loi normale pour les différentes variables. La statistique F utilisée pour le test de comparaison est définie par :

F = [n1 + n2 - (p+1)] / [(n1 + n2 - 2)p] T²

Cette statistique suit une loi de Fisher à p et n1+n2-p-1 degrés de liberté si les échantillons suivent une loi normale pour les différentes variables.

Si l'on souhaite comparer plus de deux échantillons, le test basé sur la distance de Mahalanobis peut être utilisé pour identifier les sources possibles de la différence observée au niveau global. Il est alors recommandé de faire la correction de Bonferroni pour le seuil alpha. Pour k échantillons à comparer deux à deux, on utilise alors le niveau alpha suivant :

α* = 2α / k(k-1)

Lambda de Wilks

Le lambda de Wilks est une statistique dont la particularité est de suivre la distribution de Wilks à trois paramètres.

Le Lambda de Wilks est une statistique utilsée pour tester si plusieurs groupes d'observations multivariées ont des moyennes significativement différentes.

Remarques : La distance de Mahalanobis et le lambda de Wilks peuvent être utilisé si :

1. On fait l'hypothèse que les deux échantillons variables sont distribués suivant une loi normale. Il conviendra de valider cette hypothèse avec des tests de normalité.
2. Les matrices de covariance des deux groupes sont identiques, hypothèse qu'il conviendra de valider avec les tests de Box.

Test d'égalité des matrices de covariance intra-classe

Test de Box

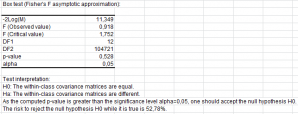
Le test de Box permet de tester l'hypothèse d'égalité des matrices de covariance intra-classe. Deux approximations ont été proposées, l'une basée sur la distribution du Khi², l'autre sur la distribution de Fisher.

Test de Kullback

Le test de Kullback permet de tester l'hypothèse d'égalité des matrices de covariance intra-classe. La statistique calculée est approximativement distribuée suivant une loi du Khi².