Tests de comparaison de moyenne t et z pour un échantillon

Principes des tests de comparaison de moyenne t de Student et z pour un échantillon

Les tests t et z pour un échantillon permettent de déterminer si la moyenne d'un échantillon est significativement différent d'une valeur D donnée (test t de Student si la variance de l'échantillon est estimée, test z si elle est connue).

Soit un échantillon de moyenne µ. Pour comparer cette moyenne à une valeur de référence, deux tests paramétriques sont possibles :

1. Le test t de Student Si on ne connaît pas la vraie variance de la population dont est extrait l'échantillon ; on utilise alors comme estimateur de la variance, la variance de l'échantillon s².
2. Le test z Si on connaît la vraie variance σ² de la population.

Ces deux tests sont dits paramétriques car leur utilisation nécessite que l'on suppose que les échantillons sont distribués suivant une loi normale. Par ailleurs, on suppose aussi que les observations sont indépendantes et identiquement distribuées. La normalité de l'échantillon peut être préalablement testée grâce aux tests de normalité.

Hypothèses des tests de comparaison de moyenne t de Student et z

Trois types de tests sont possibles en fonction de l'hypothèse alternative choisie :

• le test bilatéral :
  • H0 : µ = µ0
  • Ha : µ ≠ µ0
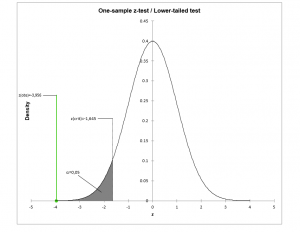
• le test unilatéral à gauche
  • H0 : µ = µ0
  • Ha : µ < µ0
• le test unilatéral à droite
  • H0 : µ = µ0
  • Ha : µ > µ0