Comparaison des variances de deux échantillons
Comparaison des variances de deux échantillons, y compris le test de Fisher, compare les variances de 2 échantillons. Exécutez-les dans Excel avec le logiciel XLSTAT.
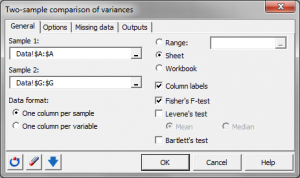
Principe du test de comparaison des varainces de deux échantillons
Soit un échantillon E1, comprenant n1 observations, de variance s1². Soit un second échantillon E2, comprenant n2 observations, de variance s2². Un test de comparaison de variance de deux échantillons étudie si les varainces s1² et s2² sont égales.
Tests de comparaison des variances dans XLSTAT
Trois tests paramétriques sont proposés pour la comparaison des variances de deux échantillons.
Remarque : les trois tests : tests de Fisher, Bartlett et Levene recquièrent des échantillons indépendants.
Test F de Fisher
Soit R le rapport supposé entre les variances (R vaut 1 lorsque l'on suppose l'égalité).
La statistique F du test est donnée par :
F = s1² ⁄ R*s2²
Cette statistique suit une loi de Fisher à (n1-1) et (n2-1) de degrés de liberté si les deux échantillons suivent une loi normale.
Trois types de tests sont possibles en fonction de l'hypothèse alternative choisie :
- le test bilatéral :
- H0 : s1² = s2²
- Ha : s1² ≠ s2²
- le test unilatéral à gauche
- H0 : s1² = s2²
- Ha : s1² < s2²
- le test unilatéral à droite
- H0 : s1² = s2²
- Ha : s1² > s2²
Test de Levene
Le test de Levene peut être utilisé pour comparer deux variances ou plus. C'est un test bilatéral pour lequel les hypothèses nulle et alternative sont dans le cas où deux variances sont comparées :
- H0 : s1² = s2²
- Ha : s1² ≠ s2²
La statistique de ce test est plus complexe que celle du test de Fisher et fait intervenir les écarts absolus à la moyenne (article original de Levene, 1960) ou à la médiane (Brown et Forsythe, 1974). L'utilisation de la moyenne est recommandée pour les distributions symétriques, à queues moyennement épaisses. L'utilisation de la médiane est recommandée pour les distributions asymétriques.
La statistique de Levene suit une loi de Fisher à 1 et n1+n2-2 degrés de liberté.
Test d'homogénéité des variances de Bartlett
Le test de Bartlett peut être utilisé pour comparer deux variances ou plus. Ce test est sensible à la normalité des données. Autrement dit, si l'hypothèse de normalité des données semble fragile, on utilisera plutôt le test de Levene ou de Fisher. En revanche, le test de Bartlett est plus performant si les échantillons suivent une loi normale. Il s'agit aussi d'un test bilatéral similaire au test de Levene qui peut être utilisé avec deux variances ou plus.
La statistique de Bartlett suit une loi du Khi² à 1 degré de liberté.


analysez vos données avec xlstat
Fonctionnalités corollaires