Pruebas t et z para dos muestras

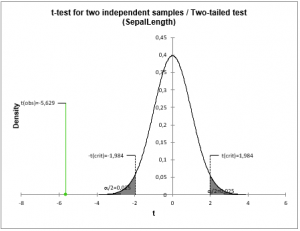
¿Qué son las pruebas t y z de dos muestras?

Las pruebas t y z de dos muestras son pruebas paramétricas muy populares en estadística. Estos métodos se utilizan ampliamente en la estadística inferencial y permiten comprobar una hipótesis general denominada hipótesis nula.

La comprobación de hipótesis es un concepto importante en estadística. La prueba Z y la prueba t de Student se utilizan para determinar el nivel de significación de un conjunto de datos. Estas dos pruebas se utilizan para comparar las medias de dos muestras, es decir, permiten comprobar la hipótesis nula de igualdad de las medias de dos grupos (muestras).

El método de cálculo difiere según la naturaleza de las muestras. Se distingue entre muestras independientes o muestras pareadas. Las pruebas t y z se conocen como paramétricas porque se asume que las muestras se distribuyen normalmente.

XLSTAT proporciona una función completa y flexible de pruebas t y z de dos muestras que propone varias opciones estándar y avanzadas que le permitirán obtener una visión profunda de sus datos:

• Ejecutar una prueba de dos muestras para muestras independientes o pareadas
• Elegir entre tres hipótesis alternativas diferentes
• Elegir el método de Monte-Carlo o el método de valor p asintótico para el cálculo del valor p
• Utilizar una prueba F para probar la igualdad de varianzas y ayudar a elegir entre la prueba t y la prueba z
• Mostrar diagramas de dominancia para hacer una comparación visual de las muestras

¿Cuál es la diferencia entre una prueba t de dos muestras y una prueba z?

Estas son las diferencias entre la prueba t de dos muestras y la prueba z:

• La prueba t se utiliza para comparar y analizar si las medias de dos poblaciones son diferentes entre sí cuando no se conoce la desviación estándar. La prueba Z, por otro lado, es una prueba paramétrica para determinar si las medias de dos conjuntos de datos difieren entre sí y se aplica cuando se conoce la desviación estándar.
• La prueba t se basa en la distribución t de Student, mientras que la prueba z se basa en el supuesto de que la distribución de las medias muestrales es normal.
• En el caso de la prueba t, la varianza de la población debe ser desconocida. Sin embargo, la varianza de la población debe conocerse o suponerse conocida en el caso de una prueba z. La prueba z se utiliza cuando el tamaño de la muestra es grande (n > 30), mientras que la prueba t es apropiada cuando el tamaño de la muestra es pequeño (n < 30).

¿Cuándo utilizar una prueba t y z de dos muestras?

Prueba t de Student

El uso de la prueba t de Student requiere que se tome una decisión de antemano sobre si las varianzas de las muestras deben considerarse iguales o no. XLSTAT da la opción de utilizar la prueba F de Fisher para probar la hipótesis nula de igualdad de las varianzas de los grupos (muestras) y utilizar el resultado de la prueba en los cálculos posteriores. Si consideramos que las dos muestras tienen la misma varianza, la varianza común se estima mediante

s² = [(n1-1)s1² + (n2-1)s2²] / (n1 + n2 - 2)

Donde s1 es la desviación estándar de la primera muestra (grupo) y s2 es la desviación estándar de la segunda muestra.

Por tanto, la estadística de la prueba viene dada por

t = (µ1 - µ2 -D) / (s √1/n1 + 1/n2)

El estadístico t sigue una distribución de Student con n1+n2-2 grados de libertad.

Si consideramos que las varianzas son diferentes, el estadístico viene dado por:

t = (µ1 - µ2 -D) / (√s1²/n1 + s2²/n2)

Prueba z

Para la prueba z, se supone que se conoce la varianza s² de la población. El usuario puede introducir este valor o estimarlo a partir de los datos (esto se ofrece sólo con fines didácticos). La estadística de la prueba viene dada por

z = (µ1 - µ2 -D) / (σ √1/n1 + 1/n2)

El estadístico z sigue una distribución normal.

Comparación de las medias de dos muestras emparejadas

Si dos muestras están emparejadas, tienen que ser del mismo tamaño. Cuando faltan valores en determinadas observaciones, se elimina la observación de ambas muestras o se estiman los valores que faltan.

Se estudia la media de las diferencias calculadas para las n observaciones. Si d es la media de las diferencias, s² la varianza de las diferencias y D la supuesta diferencia, el estadístico de la prueba t viene dado por:

T= (d-D) ⁄ (s/√n)

El estadístico t sigue una distribución de Student con n-1 grados de libertad.

Para la prueba z, el estadístico es el siguiente, donde σ² es la varianza

z= (d-D) ⁄ (σ/√n)

El estadístico z sigue una distribución normal.

Hipótesis alternativas

Son posibles tres tipos de pruebas, en función de la hipótesis nula y, por tanto, de la hipótesis alternativa elegida:

• prueba de dos colas,
• prueba de cola izquierda
• prueba de cola derecha.

Tutoriales sobre cómo ejecutar pruebas t de dos muestras y pruebas z utilizando el software XLSTAT

Aquí hay algunos tutoriales sobre cómo utilizar la prueba t de dos muestras y la prueba z:

• Un ejemplo sobre cómo ejecutar una prueba t de Student en dos muestras independientes
• Un ejemplo sobre cómo ejecutar una prueba t de Student en dos muestras pareadas