Tests d'hétéroscédasticité

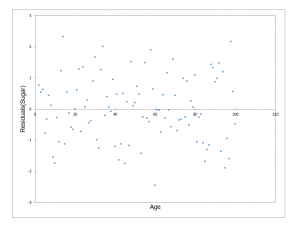
Qu’est-ce que l’hétéroscédasticité ?

Le concept d'hétéroscédasticité – son contraire étant l'homoscédasticité – est utilisé en statistique, et plus particulièrement dans le contexte de la régression linéaire ou de l'étude de séries chronologiques, pour décrire le cas où la variance des erreurs du modèle n'est pas la même pour toutes les observations, alors que souvent, l'une des hypothèses premières en modélisation est que les variances sont homogènes et que les erreurs du modèle sont identiquement distribuées.

Pourquoi l’hétéroscédasticité est-elle un problème ? En régression linéaire, le fait que les erreurs (ou résidus) du modèle ne soient pas homoscédastiques a pour conséquence que les coefficients du modèle estimés par la méthode des moindres carrés ordinaires ne sont ni sans biais ni ceux de variance minimale et l'estimation de leur variance n'est pas fiable.

Comment vérifier l’hétéroscédasticité dans XLSTAT ?

Il convient donc, si l'on soupçonne que les variances ne sont pas homogènes (une simple représentation des résidus en fonction des variables explicatives peut révéler une hétéroscédasticité), d'effectuer un test d'hétéroscédasticité. Plusieurs tests ont été mis au point, avec pour hypothèses nulle et alternative :

• H0 : Les résidus sont homoscédastiques
• Ha : Les résidus sont hétéroscédastiques

Le test de Breuch & Pagan

Ce test d’hétéroscédasticité a été développé par Breusch et Pagan (1979), puis amélioré par Koenker (1981). Pour cette raison, il est parfois connu comme le test de Breusch-Pagan et Koener. Il permet d’identifier des cas d’hétéroscédasticité, qui empêche la fiabilité des estimateurs classiques des paramètres de la régression linéaire. Si e est le vecteur des erreurs du modèle, l’hypothèse nulle H0 : “Les termes d’erreurs du modèle ont une variance constante” peut s’écrire :

H0 : E(e2) = σ2

Pour vérifier que les erreurs quadratiques sont indépendantes des variables explicatives, ce qui peut se traduire dans plusieurs formes fonctionnelles, le plus simple est de réaliser une régression des erreurs quadratiques par les variables explicatives. Si les données sont homoscédastiques, le coefficient de détermination R2 ne devrait pas être égal à 0. Si H0 n’est pas rejeté, nous pouvons conclure que l’hétéroscédasticité, si elle existe, ne prend pas la forme fonctionnelle utilisée. En pratique, l’hétéroscédasticité n’est pas un problème si H0 n’est pas acceptée. Si H0 est rejetée, c’est probable que l’hétéroscédasticité soit présente et qu’elle prend la forme fonctionnelle décrite au-dessus.

La statistique de test utilisée, proposée par Koenker (1981) est :

LM = nR2

avec LM le Multiplieur de Variance. Cette statistique de test a l’avantage de suivre asymptotiquement la distribution du Chi2 à p degrés de liberté, où p est le nombre de variables explicatives.

Si l’hypothèse nulle est rejetée, il sera nécessaire de transformer les données avant le réaliser la régression, ou d’utiliser des méthodes de modélisation afin de prendre en compte la variabilité de la variance.

Test de White et test de White modifié (Wooldridge)

Comment détecter l’hétéroscédasticité avec le test de White ? Ce test a été développé par White (1980) pour identifier des cas d’hétéroscédasticité qui rendent les estimations classiques des paramètres de la régression linéaire non fiables. L’idée est similaire à celle de Breusch et Pagan, mais s'établit sur des suppositions plus faibles par rapport à la forme prise par l’hétéroscédasticité. Cela résulte en une régression des erreurs quadratiques par les variables explicatives ainsi que leurs carrés et leurs produits deux à deux. La statistique de test est la même que dans le test de Breusch-Pagan, mais dû à la présence d’un nombre bien plus important de variables sur lesquelles on régresse, il y a 2p+p(p-1)/2* degrés de liberté pour le Chi2.

Afin d’éviter la perte de trop de degrés de liberté, Wooldrigde (2009) propose de réaliser une régression des erreurs quadratiques par les prédictions du modèle ainsi que leur carré. Cela réduit à 2 le nombre de degrés de liberté pour le Chi2.

Comment corriger l’hétéroscédasticité dans XLSTAT ?

Newey West et autres estimateurs

XLSTAT vous permet de corriger l’hétéroscédasticité. Plusieurs estimateurs (Newey West, HC0, HC1, etc) sont disponibles pour cela dans notre outil de régression linéaire.

White (1980) ainsi que d’autres auteurs ont exploré des façons de corriger l’estimation classique des covariances en utilisant les résidus et l’effet de levier centré obtenus suite à la régression linéaire (MacKinnon (1985), Zeileis (2006)). Quand les hypothèses de la régression linéaire classique ne sont pas vérifiées, même si les estimateurs des coefficients restent inchangés, l’écriture simplifiée de la matrice de covariance des paramètres bêta est impossible, et nous devons revenir à l’expression générale :

Var (β) = (XtX)-1 (Xt ΩX)(XtX)-1

Transformation de la variable dépendante

Vous pouvez utiliser l’outil de transformation de variables de XLSTAT pour appliquer une transformation de Box-Cox afin de corriger l’hétéroscédasticité.

Régression pondérée

Vous pouvez réaliser une régression pondérée dans le but de générer l’hétéroscédasticité. Tous les modèles de régression proposés dans XLSTAT permettent de sélectionner des poids dans la boîte de dialogue.

Résultats pour les tests d’hétéroscédasticité dans XLSTAT

Parmi les sorties de XLSTAT, vous trouverez :

• un tableau de statistiques descriptives
• un graphique des résidus
• les résultats des tests sélectionnés (statistique de test, valeur critique, p-valeur, alpha)

Tutoriels sur les tests d’hétéroscédasticité

Vous vous demandez comment lancer un test d’hétéroscédasticité dans Excel ? Vous pouvez suivre ce tutoriel pour voir comment configurer et interpréter un test d’hétéroscédasticité dans Excel en utilisant le logiciel XLSTAT.