Analyse descriptive des séries chronologiques

But de l'analyse descripitve des séries chronologiques

L'une des phases essentielles de l'analyse des séries chronologiques consiste à déterminer si une valeur observée à un temps t dépend de ce qui a été observé dans le passé ou non. Si la réponse est affirmative, alors l'étape suivante essaiera de répondre à comment se manifeste cette dépendance.

Fonctions d'autocovariance et d'autocorrélation

Les fonctions d'autocovariance (FACV) et d'autocorrélation (FAC) estimées sur un échantillon donnent une idée de la dépendance entre les données d'une série. La visualisation de la FAC ou de la fonction d'autocorrélation partielle (FACP) aide à l'identification de modèles susceptibles de permettre d'expliquer un phénomène sur la base de ce qui a été observé, puis de prédire des valeurs futures. Par exemple la théorie montre que pour un modèle autorégressif d'ordre p, AR(p), la fonction FACP doit être nulle pour un décalage supérieur à p.

Fonctions de corrélations croisées

Les fonctions de corrélations croisées (FCC) permettent quant à elles de lier deux séries chronologiques et de déterminer si elles covarient, et si oui, dans quelle mesure.

Les fonctions FACV, FAC, FACP, FCC sont toutes calculées par cet outil.

Bruit blanc

Une autre étape importante de l'analyse des séries chronologiques consiste en la transformation des séries de manière à ne plus obtenir qu'un bruit blanc. Obtenir un bruit signifie que l'on a réussi à supprimer les autocorrélations, et les composants déterministes impliquant les variations de la série. Plusieurs tests sont proposés par XLSTAT pour tester, sur la base de la série elle même ou de sa FAC, si elle est significativement différente d'un bruit blanc ou non (Jarque Bera, Box-Pierce, Ljung-Box, McLeod-Li).

Résultats de l'analyse descriptive des séries chronologiques avec XLSTAT

• Tests de normalité et de bruit blanc : dans ce tableau sont affichés les résultats des divers tests. Le test de normalité de Jarque-Bera est calculé une fois pour chacune des séries, alors que les tests du bruit blanc (Box-Pierce, Ljung-Box, Mcleod-Li) sont calculés pour chaque pas indiqué dans la boîte de dialogue. Le nombre de degrés de liberté (DDL), la valeur des statistiques et la p-value calculée sur la base d'une distribution du Khi²(DDL) sont affichés. Pour le test de Jarque-Bera, plus la p-value est faible, plus la normalité de l'échantillon degré est probable. Pour les trois autres tests, plus la p-value est faible, plus il est vraisemblable que les données correspondent à un bruit blanc.
• Analyse descriptive : dans ce tableau sont affichés pour chaque pas de temps les valeurs des différentes fonctions descriptives, et les intervalles de confiance correspondants.
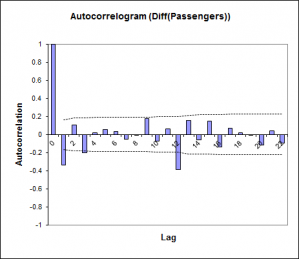
• Graphiques : pour chaque fonction sélectionnée, un graphique est affiché.

Si plusieurs séries ont été sélectionnées, on obtient les résultats suivants pour les « corrélations croisées » :

• Tests du bruit blanc : dans ce tableau sont affichés les résultats des tests de Box-Pierce, Ljung-Box, et Mcleod-Li, pour chaque nombre de pas de temps indiqué dans la boîte de dialogue. Le nombre de degrés de liberté (DDL), la valeur des statistiques et la p-value calculée sur la base d'une distribution du Khi²(DDL) sont affichés.
• Corrélations croisées : dans ce tableau sont affichées pour chaque couple de variables les corrélations croisées. Le graphique correspondant est ensuite affiché.