Classification par la méthode des nuées dynamiques (k-means)

Description de la Classification k-means dans XLSTAT

Description générale

La classification k-means a été introduite par MacQueen en 1967. D'autres algorithmes similaires ont été développés par Forgey (1965) (centres mobiles) et Friedman (1967).

La classification k-means présente notamment les avantages suivants :

• un objet peut être affecté à une classe au cours d'une itération puis changer de classe à l'itération suivante, ce qui n'est pas possible avec la classification ascendante hiérarchique pour laquelle une affectation est irréversible.
• En multipliant les points de départ et les répétitions on peut explorer plusieurs solutions possibles.

L'inconvénient de cette méthode est qu'elle ne permet pas de découvrir quel peut être un nombre cohérent de classes, ni de visualiser la proximité entre les classes ou les objets.

Les méthodes k-means et CAH sont donc complémentaires.

Remarque : dans le cas où vous souhaiteriez prendre en compte des variables qualitatives pour la classification, il est nécessaire d'effectuer au préalable une analyse des correspondances multiples (ACM) et de considérer les coordonnées des individus sur les axes factoriels obtenus comme de nouvelles variables.

Principe de la méthode k-means

La classification k-means est une méthode itérative qui, quel que soit son point de départ, converge vers une solution. La solution obtenue n'est pas nécessairement la même quel que soit le point de départ. Pour cette raison, on répète en général plusieurs fois les calculs pour ne retenir que la solution la plus optimale pour le critère choisi.

Pour la première itération on choisit un point de départ qui consiste à associer le centre des k classes à k objets (pris au hasard ou non). On calcule ensuite la distance entre les objets et les k centres et on affecte les objets aux centres dont ils sont les plus proches. Puis on redéfinit les centres à partir des objets qui ont été affectés aux différentes classes. Puis on affecte à nouveau les objets en fonction de leur distance aux nouveaux centres. Et ainsi de suite jusqu'à ce que la convergence soit atteinte.

Critères de classification

Plusieurs critères de classification peuvent être utilisés pour parvenir à une solution. XLSTAT propose quatre critères à minimiser.

Trace(W) : la trace de W, matrice d'inertie intra-classe commune (pooled SSCP matrix) est le critère le plus classique. Minimiser la trace de W pour un nombre de classes donné, revient à minimiser la variance intra-classe totale, autrement dit à minimiser l'hétérogénéité des groupes. Ce critère est sensible aux effets d'échelle. Si on ne veut pas donner plus de poids à certaines variables plutôt qu'à d'autres, on doit préalablement normaliser les données. Par ailleurs, ce critère tend à produire des classes de même taille.

Déterminant(W) : le déterminant de W, matrice de covariance intra-classe commune (pooled within covariance matrix) est un critère nettement moins sensible aux effets d'échelle que le critère trace(W). Par ailleurs, la taille des groupes peut être moins homogène qu'avec le critère de la trace.

Wilks lambda : les résultats donnés par la minimisation de ce critère sont identiques à ceux donnés par le déterminant de W. Le critère du lambda de Wilks correspond à la division du déterminant(W) par le déterminant(T) où T est la matrice d'inertie totale. La division par le déterminant de T permet d'avoir un critère toujours compris entre 0 et 1.

Trace(W) / Médiane : si l'on choisit ce critère, le barycentre d'une classe n'est pas le point moyen de la classe, mais le point médian qui correspond à un objet de la classe. L'utilisation de ce critère entraîne des calculs plus longs.

Résultats de la Classification k-means dans XLSTAT

Statistiques descriptives : le tableau des statistiques descriptives présente des statistiques simples pour toutes les variables sélectionnées. Le nombre de valeurs manquantes, le nombre de valeurs non manquantes, la moyenne, l'écart-type sont affichés pour les variables quantitatives. Pour les variables qualitatives, les catégories avec leur fréquence respective et pourcentage sont affichées.

Matrice de corrélation : ce tableau est affiché afin de vous permettre d'avoir un aperçu des corrélations entre les différentes variables sélectionnées.

Évolution de l'inertie intra-classe : si vous avez choisi un nombre de classes entre deux bornes distinctes, XLSTAT affiche dans un premier temps l'évolution de l'inertie intra-classe, qui diminue mathématiquement lorsque le nombre de classes augmente. Si les données sont distribuées de manière homogène, la décroissance est linéaire. S'il y a réellement une structure de groupes, un coude sera observé pour le nombre de classes pertinent.

Évolution du coefficient de silhouette : si vous avez choisi un nombre de classes entre deux bornes distinctes et que l'option Coefficient de Silhouette est activée, un tableau avec le graphique associé montrent l'évolution du coefficient de silhouette pour chaque k. Il est possible de choisir le nombre de classes pertinent en prenant le nombre de classes avec le coefficient de silhouette le plus proche de 1.

Bilan de l'optimisation : dans ce tableau est affichée l'évolution de la variance intra-classe. Si plusieurs répétitions ont été demandées, les résultats sont affichés pour chaque répétition. De plus, les résultats de la meilleure répétition sont affichés en gras.

Statistiques pour chaque itération : dans ce tableau est affichée l'évolution des diverses statistiques calculées au fur et à mesure des itérations de la répétition ayant donné le résultat optimal pour le critère choisi. Si l'option correspondante est activée dans l'onglet Graphiques, un graphique présentant l'évolution du critère choisi au fur et à mesure des itérations est affiché.

Décomposition de l'inertie pour la classification optimale : dans ce tableau sont affichées l'inertie intra-classe, l'inertie inter-classe et l'inertie totale.

Remarque : si les données sont centrées/réduites (option de l'onglet Options) les résultats pour le bilan de l'optimisation, les statistiques pour chaque itération et le tableau de la décomposition de l'inertie sont calculés dans l'espace centré-réduit. En revanche, les résultats qui suivent sont affichés dans l'espace d'origine si l'option « Résultats dans l'espace d'origine » est activée.

Barycentres initiaux des classes : dans ce tableau sont affichées les coordonnées des barycentres qui ont été calculées grâce à la partition initiale aléatoire ou grâce aux algorithmes K|| et K++. Dans le cas où les centres ont été définis par l'utilisateur, ce sont les centres définis qui sont affichés.

Barycentres des classes : dans ce tableau sont affichées les coordonnées des barycentres des classes pour les différents descripteurs.

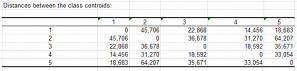
Distances entre les barycentres des classes : dans ce tableau sont affichées les distances entre les barycentres des classes pour les différents descripteurs.

Objets centraux : dans ce tableau sont affichées, pour chaque classe, les coordonnées de l'objet le plus proche du barycentre de la classe.

Distances entre les objets centraux : dans ce tableau sont affichées les distances entre les objets centraux des classes pour les différents descripteurs.

Résultats par classe : les statistiques descriptives des classes (nombre d'objets, somme des poids, variance intra-classe, distance minimale au barycentre, distance maximale au barycentre, distance moyenne au barycentre) sont affichées dans la première partie du tableau. Dans la seconde partie sont affichés les objets.

Résultats par objet : dans ce tableau est indiquée, pour chaque objet, sa classe d'affectation dans l'ordre initial des objets.

• Distance au barycentre : cette colonne indique la distance entre une observation et le barycentre de sa classe.
• Corrélations avec les barycentres : cette colonne indique la corrélation de Pearson entre une observation et le barycentre de sa classe.
• Coefficients de silhouette : cette colonne indique le coefficient de silhouette de chaque observation.

Coefficients de silhouette (Moyenne par classe) : ce tableau et le graphique associé affichent le coefficient de silhouette moyen de chaque classe et en dernière ligne le coefficient de silhouette de la classification optimale (moyenne des moyennes par classe).

Contribution (Analyse de la variance) : ce tableau permet de connaître les variables qui contribuent le plus à la séparation des classes en effectuant une ANOVA.

Profil des classes : ce graphique permet de comparer visuellement les moyennes des différentes classes créées.