Analyse Factorielle

Qu’est-ce que l'analyse factorielle ?

La méthode de l'analyse factorielle date du début du 20ième siècle (Spearman, 1904) et a connu de nombreux développements, plusieurs méthodes de calcul ayant été proposées. Si cette méthode a d'abord été utilisée par les psychométriciens, son champ d'application s'est peu à peu étendu à de nombreux autres domaines, par exemple en géologie, médecine, finance. On distingue aujourd'hui deux grands types d'analyse factorielle :

• l'analyse factorielle exploratoire (en anglais, exploratory factor analysis ou EFA)
• l'analyse factorielle confirmatoire (en anglais, confirmatory factor analysis ou CFA)

L'EFA correspond à ce qui est décrit ci-dessous et à ce qui est utilisé par XLSTAT. Il s'agit d'une méthode qui permet de découvrir l'existence éventuelle de facteurs sous-jacents synthétisant l'information contenue dans un plus grand nombre de variables mesurées. La structure liant les facteurs aux variables est inconnue a priori et seul éventuellement le nombre de facteurs est supposé.

La CFA dans sa version traditionnelle s'appuie sur un modèle identique à celui de l'EFA, mais la structure liant les facteurs sous-jacents aux variables mesurées est supposée connue. Une version plus récente de la CFA est liée aux modèles d'équations structurelles.

Analyse factorielle : Passer de p variables à k facteurs

L'exemple historique de Speaman, même s'il a depuis fait l'objet de nombreuses critiques et améliorations, permet de bien comprendre le principe et l'utilité de la méthode. En analysant les corrélations entre les notes obtenues par des enfants dans différentes matières, Spearman a voulu faire l'hypothèse que les notes dépendaient finalement d'un seul facteur, l'intelligence, avec une partie résiduelle due à un effet individuel, culturel ou autre.

Ainsi la note obtenue par l'individu (i) dans une matière (j) peut s'écrire x(i,j) = µ + b(j)F + e(i,j), avec µ la note moyenne de l'échantillon étudié, et où F est le niveau d'intelligence de l'individu (le facteur sous-jacent) et e(i,j) le résidu.

En généralisant cette écriture à p matières (les variables d'entrée) et à k facteurs sous-jacents, on obtient le modèle suivant : (1) x = µ + Λf + u où x est un vecteur de dimension (p x 1), µ est le vecteur moyen, Λ est la matrice (p x k) des coordonnées factorielles (loadings en anglais) et f et u sont des vecteurs aléatoires de dimensions respectives (k x 1) et (p x 1), que l'on suppose indépendants. Les éléments de f sont appelés facteurs communs, et ceux de u facteurs spécifiques.

Si l'on s'impose que la norme de f vaut 1, alors la matrice de covariance des variables d'entrée sur la base de l'expression (1) s'écrit (2) Σ = ΛΛ' + Ψ Ainsi, la variance de chacune des variables peut être divisée en deux parties : la communalité (car provenant des facteurs communs), (3) hi² = Σj=1..k λij², et Ψii la variance spécifique ou variance unique (car spécifique à la variable en question). On peut montrer que la méthode qui permet de calculer la matrice Λ, enjeu essentiel de l'analyse factorielle, est indépendante de l'échelle. Il est donc équivalent de travailler à partir de la matrice de covariance ou de la matrice de corrélation.

L'enjeu de l'analyse factorielle est de permettre de trouver les matrices Λ et Ψ, de telle sorte que l'équation (2) soit au moins approximativement vérifiée.

Remarque : l'analyse factorielle est parfois rapprochée de l'Analyse en Composantes Principales (ACP), car l'ACP est un cas particulier de l'analyse factorielle (cas où k le nombre de facteurs vaut p le nombre de variables). Néanmoins ces deux méthodes ne sont en général pas utilisées dans le même contexte. En effet, l'ACP est avant tout utilisée pour réduire le nombre de dimensions tout en maximisant la variabilité conservée, pour obtenir des facteurs indépendants (non corrélés), ou pour visualiser les données dans un espace à 2 ou trois dimensions. L'analyse factorielle est quant à elle utilisée pour identifier une structure latente, et pour éventuellement réduire par la suite le nombre de variables mesurées si elles sont redondantes vis-à-vis des facteurs latents.

Extraction des facteurs en analyse factorielle

Trois méthodes d'extraction des facteurs latents sont proposées par XLSTAT :

• Composantes principales : cette méthode est aussi celle utilisée en Analyse en Composantes Principales (ACP). Elle n'est proposée ici que dans un but de comparaison entre les résultats des trois méthodes, sachant que les résultats proposés dans le module dédié à l'ACP sont plus complets.
• Facteurs principaux : cette méthode est probablement la plus utilisée. C'est une méthode itérative qui permet de faire converger progressivement les communalités. Les calculs sont interrompus dès que le changement maximum des communalités est en dessous d'un seuil donné, ou lorsqu'un nombre maximal d'itérations est atteint. Les communalités initiales peuvent être calculées suivant différentes méthodes.
• Maximum de vraisemblance : cette méthode a d'abord été proposée par Lawley (1940). La proposition de l'utilisation de l'algorithme de Newton-Raphson (méthode itérative) date de Jennrich (1969). Elle a ensuite été améliorée et généralisée par Jöreskog (1977). Cette méthode fait l'hypothèse que les variables d'entrée suivent une distribution normale. Les communalités initiales sont calculées suivant la méthode proposée par Jöreskog (1977). Dans le cadre de cette méthode, un test d'ajustement est calculé. La statistique utilisée pour le test suit une loi du Khi² à (p-k)² / 2 – (p+k) / 2 degrés de liberté, où p est le nombre de variables et k le nombre de facteurs.

Nombre de facteurs utilisée en analyse factorielle

La détermination du nombre de facteurs à retenir est l'un des enjeux de l'analyse factorielle. La méthode « automatique » proposée par XLSTAT est uniquement basée sur la décomposition spectrale de la matrice de corrélation et sur la détection d'un seuil à partir duquel l'apport d'information (au sens de la variabilité) n'est pas significatif. Si la méthode du maximum de vraisemblance propose un test d'ajustement pour aider à déterminer quel est le bon nombre de facteurs principaux, pour la méthode des facteurs principaux les méthodes sont plus empiriques.

La règle de Kaiser-Guttman propose de ne retenir que les facteurs pour lesquels les valeurs propres associées sont supérieurs strictes à 1 (les calculs doivent alors être effectués sur la matrice des corrélations). Le scree test (Cattell, 1966) est fondé sur la courbe décroissante des valeurs propres. Le nombre de facteurs à retenir correspond au premier point d'inflexion détecté sur la courbe. Des méthodes de validation croisée ont aussi été proposées dans ce but.

Cas problématiques (Heywood cases)

Les communalités sont par définition des carrés de corrélations. Elles doivent donc être comprise entre 0 et 1. Néanmoins, il se peut que les algorithmes itératifs (méthode des facteurs principaux ou du maximum de vraisemblance) engendrent des solutions pour lesquelles les communalités sont égales à 1 (Heywood cases) ou supérieures à 1 (ultra Heywood cases). Les raisons de telles anomalies peuvent être multiples (trop de facteurs, pas assez de facteurs, …). Lorsque de tels cas sont rencontrés XLSTAT fixe les communalités à 1 et adapte en conséquence les éléments de L.

Rotations en analyse factorielle

Une fois les résultats obtenus, il est possible de les transformer afin de les rendre plus facilement interprétables, par exemple en essayant de faire en sorte que les coordonnées des variables sur les facteurs soient ou élevées (en valeur absolue), ou proches de zéro. On distingue deux grandes familles de rotations :

• les rotations orthogonales peuvent être utilisées lorsque les facteurs ne sont pas corrélés (d'où orthogonales). Les méthodes proposées par XLSTAT sont Varimax, Quartimax, Equamax, Parsimax, Orthomax. La rotation Varimax est la plus utilisée. Elle permet de faire en sorte que pour chaque facteur, il y ait peu de coordonnées factorielles (loadings) élevées, et beaucoup de faibles. L'interprétation est ainsi facilitée puisqu'en principe les variables initiales seront surtout associées à l'un des facteurs.
• les transformations obliques peuvent être utilisées lorsque les facteurs sont corrélés (d'où obliques). Les méthodes proposées par XLSTAT sont Quartimin et Oblimin.

La méthode Promax, également proposée par XLSTAT, est une procédure mixte puisqu'elle consiste d'abord en une rotation Varimax, puis en une rotation oblique telle que les coordonnées factorielles (loadings) élevées et faibles soient les mêmes, mais avec les valeurs faibles encore plus faibles.

Résultats de l'analyse factorielle

• Matrice de corrélation/de covariance : ce tableau correspond aux données qui sont ensuite utilisées pour les calculs. Le type de corrélation dépend du choix de l’utilisateur. Les corrélations significatives sont affichées en gras.
• Alpha de Cronbach.
• Changement maximum de communalité à chaque itération : ce tableau permet d'observer l'évolution du changement maximum de communalité pour les 10 dernières itérations. Dans le cas de la méthode du maximum de vraisemblance, l'évolution d'un critère proportionnel à l'opposé du maximum de vraisemblance est aussi affichée.
• Test d'ajustement : pour le cas où la méthode du maximum de vraisemblance.
• Matrice des corrélations reproduites : cette matrice est le produit de la matrice des coordonnées factorielles par sa transposée.
• Matrice de corrélation résiduelle : cette matrice est calculée comme la différence entre la matrice de corrélation des variables, et la matrice des corrélations reproduites.
• Valeurs propres : dans ce tableau sont affichées les valeurs propres associées aux différents facteurs, ainsi que les pourcentages et pourcentages cumulés correspondants.
• Vecteurs propres.
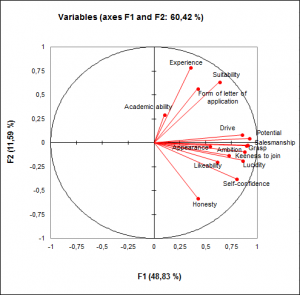
• Coordonnées factorielles : dans ce tableau sont affichées les coordonnées factorielles (coordonnées des variables dans l'espace des facteurs, appelées factor loadings ou factor pattern en anglais). Le graphique correspondant est affiché.
• Corrélations entre Variables et Facteurs.
• Coefficients du modèle factoriel : dans ce tableau sont affichés les coefficients du modèle factoriel. La multiplication des coordonnées (centrées et réduites) des observations dans l'espace d'origine par ces coefficients permet d'obtenir les coordonnées des observations dans l'espace des facteurs. Dans le cas d’une rotation, les résultats de la rotation sont affichés, avec en premier la matrice de rotation appliquée aux coordonnées des variables. Suivent ensuite les pourcentages modifiés de variabilité associés à chacun des axes concernés par la rotation. Dans les tableaux suivants sont affichées les coordonnées des variables et des observations après rotation.
• Structure factorielle : dans ce tableau sont affichées les corrélations entre les variables et les facteurs après rotation.