Analyse Factorielle des Correspondances (AFC)
L'analyse des correspondances est une méthode statistique utilisée pour étudier la relation entre deux variables qualitatives. Faites-le dans Excel avec le logiciel XLSTAT.
Qu’est-ce que l’Analyse Factorielle des Correspondances ?
L'Analyse Factorielle des Correspondances (AFC) est une méthode qui permet d'étudier l'association entre deux variables qualitatives. Cette méthode est basée sur l'inertie.
Le but de l'Analyse Factorielle des Correspondances consiste à représenter un maximum de l'inertie totale sur le premier axe factoriel, un maximum de l'inertie résiduelle sur le second axe, et ainsi de suite jusqu'à la dernière dimension. On montre que le nombre de dimensions de l'espace de représentation est inférieur ou égal à min(m1, m2)-1.Q
Quatre approches de l'Analyse Factorielle des Correspondances sont proposées :
Analyse Factorielle des Correspondances classique (AFC)
Analyse Non Symétrique des Correspondances (ANSC)
Analyse Factorielle des Correspondances utilisant la distance de Hellinger (HD)
Analyse des Correspondances Détendancée (ACD)
Analyse Non Symétrique des Correspondances
L'Analyse Non Symétrique des Correspondances (ANSC) proposée par Lauro et D'Ambra (1984) permet d'étudier l'association entre les lignes et les colonnes d'un tableau de contingence tout en introduisant la notion de dépendance entre les lignes et les colonnes, d'où l'asymétrie.
L'algorithme de XLSTAT permet de calculer l'Analyse Factorielle des Correspondances et l'Analyse Non Symétrique des Correspondances d'une manière similaire.
L’analyse d’un sous-ensemble avec l’Analyse Factorielle des Correspondances
L'analyse d'un sous-ensemble de modalités (ou catégories), est une méthode très récemment mise au point par Greenacre et Pardo (2006), qui permet de focaliser l'étude sur quelques catégories uniquement, tout en prenant en compte toutes les données du tableau de contingence grâce au maintien des sommes marginales du tableau. Sur des tableaux de taille importante cela permet de découper l'analyse en plusieurs sous-analyses.
L'Analyse des Correspondances Détendancée (ACD)
L'Analyse des Correspondances Détendancée (ACD) est une méthode proposée par Hill et Gauch (1980), principalement utilisée sur des données écologiques. L'objectif de cette méthode est de corriger deux inconvénients rencontrés lors de l'utilisation de l'AFC classique : l’ "effet d'arc" et la compression des distances entre les points se trouvant aux extrémités des axes.
Résultats de l’Analyse Factorielle des Correspondances
- Tableau de contingence : le tableau de contingence est affiché. Le diagramme en bâtons en 3 dimensions en est la représentation graphique.
- Inertie par case : le tableau des inerties par case est affiché. La somme des inerties est égale à la statistique du khi² divisée par la fréquence totale (somme des cellules du tableau de contingence).
- Test d'indépendance entre les lignes et les colonnes : ce test permet de déterminer, sur la base de la statistique du khi², si l'on doit rejeter l'hypothèse nulle selon laquelle les lignes et les colonnes du tableau sont indépendantes. Une interprétation détaillée est fournie automatiquement.
- Valeurs propres et pourcentages d'inertie : les valeurs propres et le graphique (scree plot) correspondant sont affichés. Seules les valeurs propres non triviales sont affichées. Si un filtrage a été demandé, il est appliqué aux résultats qui suivent. Remarque : la somme des valeurs propres affichées est égale à l'inertie totale. A chaque valeur propre correspond un axe principal représentant un pourcentage donné de l'inertie totale. On peut ainsi mesurer le pourcentage cumulé d'inertie totale correspondant à un nombre croissant de dimensions.
Une série de résultats est ensuite affichée, d'abord pour les points lignes, puis pour les points colonnes :
- Poids, distances et distances quadratiques à l'origine, inerties et inerties relatives : ce tableau contient des statistiques de base pour les points-lignes (puis les points-colonnes).
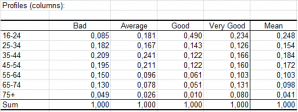
- Profils : dans ce tableau sont affichés les profils, ainsi que la moyenne des profils.
- Distances du khi² : dans ce tableau sont affichées les distances du khi² entre les profils.
- Coordonnées principales : dans ce tableau sont affichées les coordonnées principales. Ces coordonnées sont utilisées pour la création des graphiques symétriques (ou barycentriques) et asymétriques (ou pseudo-barycentriques).
- Coordonnées standard : ces coordonnées correspondent aux précédentes à un facteur près. Le facteur est la racine carrée de l'inverse de la valeur propre correspondante. Ces coordonnées sont utilisées pour la création des graphiques asymétriques (ou barycentriques).
- Contributions : les contributions sont une aide à l'interprétation. Les modalités ayant influencé le plus la construction des axes sont celles dont les contributions sont les plus élevées. On pourra se contenter d'interpréter les résultats des modalités pour lesquelles les contributions sont supérieures aux poids relatifs affichés dans la première colonne.
- Cosinus carrés : comme pour les autres méthodes factorielles, l'analyse des cosinus carrés permet d'éviter des erreurs d'interprétation dues à des effets de projection. Si les cosinus carrés associés aux axes utilisés sur un graphique sont faibles, on évitera d'interpréter la position du point-ligne ou du point-colonne correspondant.
Résultats graphiques pour l’Analyse Factorielle des Correspondances
Les graphiques constituent le but ultime de l'Analyse Factorielle des Correspondances, car ils permettent d'accélérer considérablement l'interprétation des résultats.
- Graphiques symétriques : aussi appelés représentations barycentriques, ces graphiques utilisent exclusivement les coordonnées principales. En fonction des choix effectués dans la boîte de dialogue, sont affichés, un graphique symétrique mélangeant points-lignes et points-colonnes, un graphique des points-lignes, et un graphique des points-colonnes. Le pourcentage d'inertie correspondant à chacun des axes concernés et le pourcentage d'inertie cumulée du graphique sont affichés. La proximité entre deux modalités sur le graphique est représentative de leur association.
- Graphiques asymétriques : aussi appelés représentations pseudo-barycentriques, ces graphiques utilisent d'une part les coordonnées principales (pour les points-lignes ou les points-colonnes) et d'autre part les coordonnées standard (respectivement pour les points-colonnes ou les points-lignes). Le pourcentage d'inertie correspondant à chacun des axes concernés et le pourcentage d'inertie cumulée du graphique sont affichés. Le nom du graphique, par exemple « graphique asymétrique des lignes » indique les points qui font l'objet d'une interprétation : sur un « graphique asymétrique des lignes », on étudiera la façon dont les points lignes sont positionnés par rapport aux vecteurs des modalités, ces derniers donnant des directions. Si deux points-lignes sont dans la direction d'un vecteur modalité, la modalité correspondant au point-ligne qui est le plus éloigné de l'origine est celle qui est la plus liée à la modalité correspondant au vecteur.
- Biplots de contribution : ces biplots, mis au point par Greenacre, permettent d'éviter certains problèmes des graphiques asymétriques, tout en faisant ressortir les points contribuant le plus à la construction de l'axe (les points-colonnes dans le cas d'un biplot de contribution sur les lignes et vice-versa).


analysez vos données avec xlstat
Fonctionnalités corollaires