Analyse des Correspondances Multiples (ACM ou AFCM)
Analyse des Correspondances Multiples (ACM ou AFCM) vous permet d'explorer de vastes ensembles de données de variables qualitatives. Faites-le dans Excel avec le logiciel statistique complémentaire XLSTAT.
Qu’est-ce que l’Analyse des Correspondances Multiples ?
L'Analyse des Correspondances Multiples (ACM) est une méthode qui permet d'étudier l'association entre au moins deux variables qualitatives.
L’Analyse des Correspondances Multiples est aux variables qualitatives ce que l'Analyse en Composantes Principales est aux variables quantitatives. Elle permet en effet d'aboutir à des cartes de représentation sur lesquelles on peut visuellement observer les proximités entre les catégories des variables qualitatives et les observations.
Principe de l’Analyse des Correspondances Multiples
La construction du tableau disjonctif complet est l'une des étapes préalables au calcul de l’Analyse des Correspondances Multiples. Les p variables qualitatives sont éclatées en p tableaux disjonctifs Z1, Z2, …, Zp, composés d'autant de colonnes qu'il y a de modalités pour chacune des variables. A chaque fois qu'une modalité m de la jème variable correspond à un individu i, on affecte 1 à Zj(i,m). Les autres valeurs de Zj sont nulles. Les p tableaux disjonctifs sont alors concaténés en un tableau disjonctif complet.
A partir du tableau disjonctif complet sont calculées les coordonnées des modalités des variables qualitatives, ainsi que les coordonnées des observations dans un espace de représentation optimal pour le critère d'inertie. Dans le cas de l’Analyse des Correspondances Multiples on montre que l'inertie est égale au nombre moyen de modalités moins un. Elle ne dépend donc pas uniquement de l'association entre les variables. Greenacre (1993) a proposé une mesure ajustée de l'inertie, inspirée de la Joint Correspondence Analysis (JCA). Cet ajustement permet d'avoir des pourcentages plus élevés et plus informatifs pour les axes de représentation.
L’analyse d’un sous-ensemble de modalités par l’Analyse des Correspondances Multiples
L'analyse d'un sous-ensemble de modalités (ou catégories), est une méthode très récemment mise au point par Greenacre et Pardo (2006), qui permet de focaliser l'étude sur quelques catégories uniquement, tout en prenant en compte toutes les données du tableau de données initial. XLSTAT vous permet de sélectionner les catégories sur lesquelles vous souhaitez focaliser l'analyse.
Résultats de l’Analyse des Correspondances Multiples
- Tableau disjonctif : ce tableau n'est affiché que si les données d'entrée correspondent à un tableau observations/variables. Ce tableau est un tableau intermédiaire permettant d'aboutir au tableau de contingence des deux variables sélectionnées.
- Tableau de Burt : le tableau de Burt est affiché si l'option correspondante a été activée. Le diagramme en bâtons en 3 dimensions en est la représentation graphique.
- Valeurs propres et pourcentages d'inertie : les valeurs propres, les pourcentages d'inertie et les pourcentages d'inertie ajustée et le graphique correspondant (scree plot) sont affichés. Seules les valeurs propres non triviales sont affichées. Si un filtrage a été demandé il est appliqué aux résultats qui suivent.
Une série de résultats est ensuite affichée, d'abord pour les variables, puis pour les observations :
- Coordonnées principales : dans ce tableau sont affichées les coordonnées principales. Ces coordonnées sont utilisées pour la création des graphiques symétriques (ou barycentriques) et asymétriques (ou pseudo-barycentriques) où elles représentent les projections des profils.
- Coordonnées standard : ces coordonnées correspondent aux précédentes à un facteur près. Le facteur est la racine carrée de l'inverse de la valeur propre correspondante. Ces coordonnées sont utilisées pour la création des graphiques asymétriques (ou pseudo-barycentriques) où elles représentent les projections des profils normés.
- Contributions : les contributions sont une aide à l'interprétation. Les modalités ayant influencé le plus la construction des axes sont celles dont les contributions sont les plus élevées. On pourra se contenter d'analyser les contributions qui sont supérieures aux poids relatifs affichés dans la seconde colonne.
- Cosinus carrés : comme pour les autres méthodes factorielles, l'analyse des cosinus carrés permet d'éviter des erreurs d'interprétation dues à des effets de projection. Si les cosinus carrés associés aux axes utilisés sur un graphique sont faibles, on évitera d'interpréter la position de l'observation ou de la variable en question.
Graphiques de l'Analyse des Correspondances Multiples
Les graphiques constituent le but ultime de l'Analyse des Correspondances Multiples, car ils permettent d'accélérer considérablement l'interprétation des données.
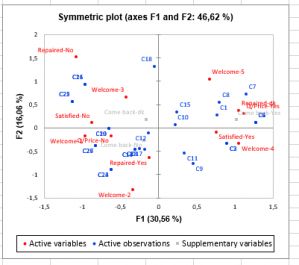
- Graphiques symétriques : aussi appelés représentations barycentriques, ces graphiques utilisent exclusivement les coordonnées principales. En fonction des choix effectués dans la boîte de dialogue, sont affichés, un graphique symétrique mélangeant observations et variables, un graphique des observations, et un graphique des variables. Le pourcentage d'inertie ajustée correspondant à chacun des axes concernés et le pourcentage d'inertie ajustée cumulée du graphique sont affichés.
- Graphiques asymétriques : aussi appelés représentations pseudo-barycentriques, ces graphiques utilisent d'une part les coordonnées principales pour les observations et d'autre part les coordonnées standard pour les variables, et réciproquement. Le pourcentage d'inertie ajustée correspondant à chacun des axes concernés et le pourcentage d'inertie ajustée cumulée du graphique sont affichés. Sur un « graphique asymétrique des observations », on étudiera la façon dont les observations sont positionnées par rapport aux vecteurs des modalités, ces derniers indiquant des directions. Si deux observations sont dans la direction d'un vecteur modalité, l'observation qui est la plus éloignée de l'origine est celle pour laquelle la modalité a le plus vraisemblablement été choisie.


analysez vos données avec xlstat
Fonctionnalités corollaires