Modèle à risques proportionnels de Cox
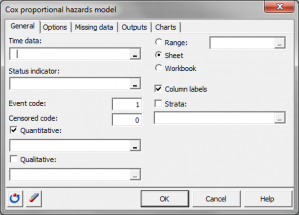
Principe du modèle de Cox
Le modèle de Cox est la méthode la plus utilisée dans le cadre de l'analyse des données de survie. Celui-ci permet de modéliser des temps de survie avec des données censurées. Elle est très utilisée dans le domaine médical (temps de survie ou de guérison d'un patient).
Le principe du modèle de Cox est de relier la date d'arrivée d'un évènement à des variables explicatives. Par exemple, dans le domaine médical, on cherche à évaluer l'impact d'un prétraitement sur le temps de guérison d'un patient.
Modèles de Cox
Le modèle de Cox se rapproche des modèles de régression classique dans le sens où l'on tente de relier un événement (modélisé par une date) à un certain nombre de variables explicatives.
Le modèle de Cox est considéré comme un modèle semi-paramétrique, il est basé sur l'hypothèse des risques proportionnels.
Le modèle de Cox s'applique à toute situation où l'on étudie le délai de survenue d'un événement. Cet événement peut être la récidive d'une maladie, la réponse à un traitement, le décès, etc. Pour chaque sujet, on connaît la date des dernières nouvelles et l'état par rapport à l'événement étudié.
Les sujets pour lesquels on ne connaît pas l'état à la date de fin de l'étude constituent des données censurées. Les valeurs des variables explicatives Xj sont notées pour chaque sujet à la date de son entrée dans l'étude.
La variable considérée T est le temps écoulé jusqu'à la survenue de l'événement étudié. Le modèle de Cox permet d'exprimer le risque instantané de survenue de l'événement en fonction de l'instant t et des variables explicatives Xj. Ces variables peuvent représenter des facteurs de risque, des facteurs pronostiques, des traitements, des caractéristiques intrinsèques au sujet, ...
Le risque instantané de survenue de l'événement λ(t, X1, X2, ..., Xp) représente la probabilité d'apparition de l'événement dans un intervalle de temps [t, t+Dt] sachant que l'événement ne s'est pas réalisé avant l'instant t. Le modèle de Cox exprime λ (t, X1, X2, ...,Xp) sous la forme :
λ(t,X) = λ0(t) exp(βX)
Cette formule appelle quelques commentaires. Le risque instantané se décompose en 2 termes dont l'un dépend du temps t et l'autre des variables Xj. Si, par exemple, les variables Xj représentent des facteurs de risque et si elles sont toutes égales à 0, λ0(t) est le risque instantané de sujets ne présentant aucun facteur de risque. La forme de λ0(t) n'étant pas précisée, c'est plutôt l'association entre les variables Xj et la survenue de l'événement considéré qui est l'intérêt central du modèle. Cela revient à déterminer les coefficients βj.
Le rapport des risques instantanés de 2 individus dont les caractéristiques respectives sont (X1, X2, ..., Xp) et (X1’, X2’, ..., Xp’) ne dépend pas du temps. De tels modèles sont dits à risques proportionnels. C'est une hypothèse importante du modèle de Cox. Si βj est positif et si 2 sujets ne diffèrent que par la j-ième caractéristique, des valeurs élevées de la j-ième caractéristique sont associées à un risque instantané plus élevé. Inversement si βj est négatif, des valeurs élevées de la j-ième caractéristique sont associées à un risque instantané plus faible.
Le modèle est estimé en utilisant le principe du maximum de vraisemblance avec quelques modifications, la fonction utilisée est appelée la vraisemblance partielle et a été introduite par Cox (1972). Comme le terme λ0(t) ne nous intéresse pas, il ne sera pas estimé, on minimisera donc une log-vraisemblance partielle :
log[L(β)] = Σi=1..n βXi - log[Σj=t(j)≥ t(i) exp(βXj)]
Contrairement à la régression linéaire, une solution analytique exacte n'existe pas. Il est donc nécessaire d'utiliser un algorithme itératif. XLSTAT utilise un algorithme de Newton-Raphson. L'utilisateur peut modifier s'il le souhaite le nombre maximum d'itérations et le seuil de convergence.
Les strates dans le modèle de Cox
Lorsque l'hypothèse de risques proportionnels n'est pas tenable, il arrive souvent que l'on stratifie le modèle. Si l'hypothèse est tenable sur des sous-échantillons alors on estime la vraisemblance partielle sur chaque sous-échantillon et on prend la somme des vraisemblances partielles. Dans XLSTAT, les strates doivent être définies par une variable qualitative.
Contraintes pour les variables qualitatives dans le modèle de Cox
Le traitement des variables qualitatives se fait en utilisant un tableau disjonctif complet. Néanmoins l'une des modalités de chaque variable doit être supprimée lors de l'estimation pour éviter la dépendance des variables. Dans le cadre d'XLSTAT, c'est la première modalité de chaque variable qualitative qui est supprimée, ainsi l'effet de la première modalité correspond à un standard. L'impact des autres modalités se fait relativement à cette première modalité omise.
Prise en compte des égalités dans le modèle de Cox
Le modèle de Cox a été conçu pour traiter des données de date continues. Néanmoins dans la pratique, il arrive souvent que plusieurs observations se produisent à la même date. Dans ce cas des adaptations de la vraisemblance partielle existent. XLSTAT en propose deux :
- La méthode de Breslow (1974) (méthode par défaut) : La vraisemblance a alors la forme suivante : log[L(β)] = Σi=1..T β Σl=1..diXl - di log[Σj=t(j)≥ t(i) exp(βXj)],, où T représente le nombre de dates différentes et di est le nombre d'observations au temps t(i).
- La méthode d'Efron (1977) : La vraisemblance partielle a alors la forme suivante : log[L(β)] = Σi=1..T β Σl=1..diXl - Σr=0..di-1 log [Σj=t(j)≥ t(i) exp(βXj) – r/di Σj=1..di exp(βXj)], où T représente le nombre de dates différentes et di est le nombre d'observations au temps t(i). Lorsqu'il n'y a pas d'égalité, ces vraisemblances partielles reviennent à la vraisemblance partielle de Cox.
Résultats pour le modèle de Cox dans XLSTAT
XLSTAT propose en autre les résultats suivant pour le modèle de Cox :
- Coefficients d'ajustement : dans ce tableau est affichée une série de statistiques pour le modèle indépendant (correspondant au cas où il n'y aurait aucune variables dans le modèle) et pour le modèle ajusté.
- Observations : le nombre total d'observations prises en compte ;
- DDL : degrés de liberté ;
- -2 Log(Vrais.) : le logarithme de la fonction de vraisemblance associée au modèle ;
- AIC : le critère d'information d'Akaike (Akaike's Information Criterion) ;
- SBC : le critère bayésien de Schwarz (Schwarz's Bayesian Criterion) ;
- Itérations : nombre d'itérations nécessaires à la convergence de l'algorithme.
- Test de l'hypothèse nulle H0 : beta=0 : l'hypothèse H0 correspond au modèle indépendant (sans variables explicatives) ; on cherche à vérifier si le modèle ajusté est significativement plus performant que ce modèle. Trois tests sont proposés : le test du rapport des vraisemblance (-2 Log(Vrais.)), le test du Score, et le test de Wald. Les trois statistiques suivent une loi du Khi² dont les degrés de liberté sont indiqués.
- Paramètres du modèle : pour chaque variable sont affichés l'estimation du paramètre, l'écart-type correspondant, le Khi² de Wald, la p-value correspondante. Par ailleurs, le rapport de risque (exponentielle du coefficient) est donné ainsi qu'un intervalle de confiance associé.
- Les résidus sont donnés pour chaque observation.


analysez vos données avec xlstat
Inclus dans
Fonctionnalités corollaires