Modèle Logit conditionnel

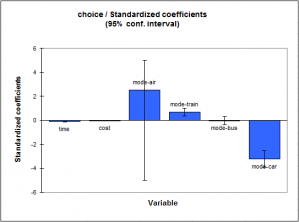
Principe du modèle Logit conditionnel

La régression logistique conditionnelle est une méthode surtout utilisée dans sa forme évoluée dans le cadre de l’analyse conjointe, elle est néanmoins utile lorsqu’on analyse un certain type de données. C’est McFadden (1973) qui a introduit ce modèle.

Au lieu d’avoir une ligne par individu, on aura une ligne par choix possible. Ainsi, ce ne sont plus les caractéristiques des individus qui sont modélisées mais celles des différentes alternatives. Ainsi, si on cherche à étudier des habitudes de transport, par exemple, on aura quatre types de transports (voiture / train / avion / vélo), chacun de ces type de transport à des caractéristiques (son prix, son coût environnemental…), mais un individu ne choisira qu’un seul des quatre moyens de transport.

Dans le cadre d’un modèle logit conditionnel, on aura pour N individus, N*4 lignes avec 4 lignes pour chaque individu associé à chacun des moyens de transport. La variable réponse binaire indiquera le choix de l’individu (1) et 0 si l’individu n’a pas choisi cette option. Il faudra aussi sélectionner une colonne associée au nom des individus (avec 4 lignes par individu pour l’exemple des moyens de transport). Les variables explicatives devront aussi avoir N*4 lignes.

Le modèle Logit conditionel

La régression logistique conditionnelle est basée sur un modèle proche de celui de la régression logistique. La différence vient de ce que tous les individus sont soumis à différentes situations avant d’exprimer leur choix (sous forme d’une variable binaire qui constitue la variable dépendante). Le fait de savoir que ce sont les mêmes individus qui ont répondu apporte de l’information que le modèle de régression logistique conditionnelle permet de prendre en compte (NB : les observations ne sont pas indépendantes à l’intérieur d’un même bloc correspondant au même individu).

La probabilité qu’un individu i choisisse le produit j est donnée par :

P_ij = e^{β^Tz_ij} / Σ_ke^{β^Tz_ik}

A partir de cette probabilité, on calcule une fonction de vraisemblance :

l(β) = Σ_i=1..nΣ_j=1..J y_ij log(P_ij)

Avec y variable binaire indiquant le choix de l’individu i pour le produit j et J nombre de choix offerts à chaque individu. Pour estimer les paramètres β du modèle (les coefficients de la fonction linéaire), on cherche à maximiser la fonction de vraisemblance. Contrairement à la régression linéaire, une solution analytique exacte n’existe pas. Il est donc nécessaire d’utiliser un algorithme itératif. XLSTAT utilise un algorithme de Newton-Raphson.