Projective mapping data analysis
Use this function to analyze projective mapping data in a quick and efficient way. Available in Excel using the XLSTAT software.
What is projective mapping data analysis
The projective mapping (or Napping) task is one of the so-called "rapid" tests that are becoming increasingly popular in the context of the sensory characterization of products. You ask each subject to place products on a sheet of paper. The data collected are simply the coordinates of the products on the x-axis and y-axis of the sheet of paper. Each subject brings a table with nn rows (one per product) and 2 columns. These data can be analyzed with the STATIS method or with Multiple Factor Analysis (MFA). While both methods have the primary objective of synthesizing information to graphically represent the products, they also allow you to determine relationships between the subjects' answers.
Options of a projective mapping data analysis in XLSTAT
Structure of the data
Each row represents a product and the columns are the x-axis and y-axis coordinates for each subject. The data of the subjects are merged vertically.
Interpreting the results
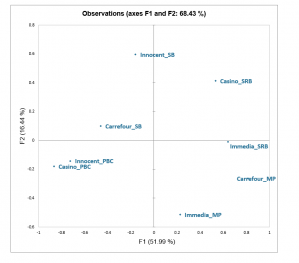
The representation of the products in the space of k factors allows you to visually interpret the proximities between the products, by means of precautions.
We can consider that the projection of a product on a plane is reliable if it is far from the center of the graph.
Number of factors
Two methods are commonly used to determine how many factors must be retained for the interpretation of the results:
Watch the decreasing curve of eigenvalues. The number of factors k to be kept corresponds to the first turning point found on the curve.
We can also use the cumulative variability percentage represented by the factor axes and decide to use only a certain percentage.
Graphic representations
These representations are only reliable if the sum of the variability percentages associated with the axes of the representation space are sufficiently high. If this percentage is high (for example 80%), the representation can be considered reliable. If the percentage is low, a good idea to produce representations on several axis pairs in order to validate the interpretation made on the two first factor axes.
Results of a projective mapping data analysis in XLSTAT
Summary statistics: The summary statistics table presents simple statistics for all selected assessors.
STATIS:
These results only concern the STATIS analysis, and are only available if this is the method you have chosen:
Eigenvalues and percentages of inertia: The eigenvalues and corresponding chart (scree plot) are displayed.
Consensus coordinates: Consensus coordinates in the factors space are displayed, with the corresponding charts (depending on the number of factors chosen).
RV matrix: The matrix of RV coefficients between all assessors is displayed. The RV index is a coefficient of similarity between two assessors included between 0 and 1. The closer it is to 1, the stronger the similarity. This matrix is used by STATIS to calculate the weights of the assessors.
Scaling factor for each assessor: The scaling factors are displayed with the associated bar chart. These scaling factors standardize the use of each subject's sheet. The less space a subject has between its products, the larger its scaling factor.
Weight of each assessor: The weights calculated by STATIS are displayed with the associated bar chart. The greater the weight, the more the assessor contributed to the consensus. Knowing that STATIS gives more weight to the closest assessors from a global point of view, a much lower weight than the others will mean that the assessor is atypical.
Consensus configuration: The consensus configuration is displayed. It corresponds to the sum of the pre-processed assessor data weighted by the weights of these assessors.
Homogeneity: The homogeneity of the assessors is displayed. It is a value between 1/m (m is the number of assessors) and 1, which increases with the homogeneity of the assessors.
RV index between each assessor and the consensus: The RV coefficients between the assessor and the consensus are displayed, with the associated bar chart. Like the weights of STATIS, these coefficients make it possible to detect atypical assessors. The advantage of these coefficients is that they are between 0 and 1, so they are easier to interpret than the weights.
Global error: The global error of the STATIS criterion is displayed. It corresponds to the sum of all residuals (which can be presented by assessor or product).
Residual per assessor: This table and the corresponding bar chart make it possible to visualize the distribution of the residual per assessor. It is thus possible to identify for which assessors STATIS has been less efficient, or in other words, which assessors stand out the most from the consensus.
Residual per product: This table and the corresponding bar chart make it possible to visualize the distribution of the residual per product. It is thus possible to identify for which products STATIS has been less efficient, or in other words, which products stand out the most from the consensus from one subject to another.
Charts of the projected points: The projected points correspond to the projections of the products of each assessor in the factor space. The representation of the projected points superimposed with those of the objects makes it possible to visualize at the same time the diversity of the information brought by the various assessors for a given product, and to visualize the relative distances from two objects according to the various assessors.
Multiple Factor Analysis:
These results only concern the MFA, and are only available if this is the method you have chosen:
Eigenvalues and percentages of inertia: The eigenvalues and corresponding chart (scree plot) are displayed.
Product coordinates: The coordinates of the products in the factors space are displayed with the corresponding charts (depending on the number of factors chosen).
Product contributions: The contributions of the products are displayed. The contributions are helpful for interpreting the plots. The products that have most influenced the calculation of the axes are those that have the higher contributions.
Squared cosines: The projection of a point on an axis, a plane or a 3-dimensional space can be considered reliable if the sum of the cosines squared on the axes of representation is not too far from 1. The cosines squared are displayed in the results proposed by XLSTAT in order to avoid any misinterpretation.
Lg coefficients: the Lg coefficients of the link between the subjects are used to measure how close the subjects are to each other.
Charts of the projected points: The projected points correspond to the projections of the products of each assessor in the factor space. The representation of the projected points superimposed with those of the objects makes it possible to visualize at the same time the diversity of the information brought by the various assessors for a given product, and to visualize the relative distances from two objects according to the various assessors.
Example of a projective mapping data analysis in XLSTAT
A tutorial on how to use projective mapping data analysis is available on our helpcenter.


analysieren sie ihre daten mit xlstat
Enthalten ind
Verwandte Funktionen