Puissance statistique pour le modèle de Cox

Puissance statistique pour le modèle de Cox

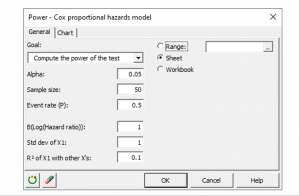
XLSTAT-Life Sciences propose un outil permettant d'appliquer le modèle à risques proportionnels de Cox sur des données de survie. XLSTAT-Power permet d'estimer la puissance ou de calculer le nombre d'observations nécessaires dans le cadre de cette approche.

Lorsqu'on teste une hypothèse à l'aide d'un test statistique, on a plusieurs éléments à choisir :

• L'hypothèse nulle H₀ et l'hypothèse alternative H_a.
• Le test statistique à utiliser
• L'erreur de première espèce (erreur de type I) que l'on appelle aussi alpha. Elle se produit lorsqu'on rejette l'hypothèse nulle alors qu'elle est vraie. Elle est fixée à priori pour chaque test et vaut 5%.

L'erreur de seconde espèce ou beta est moins étudiée mais elle revêt une grande importance. En effet, elle représente la probabilité que l'on ne rejette pas l'hypothèse nulle alors qu'elle est fausse. On ne peut pas la fixer à priori mais on peut essayer de la minimiser, en jouant sur les autres paramètres du modèle.

La puissance d'un test est calculée comme 1-beta et représente la probabilité que l'on rejette l'hypothèse nulle alors qu'elle est bien fausse. On voudra donc maximiser la puissance du test. Le module XLSTAT-Power permet de calculer cette puissance (ainsi que beta) lorsque les autres paramètres du test sont connus. D'autre part, il permet pour une puissance donnée d'évaluer la taille de l'échantillon nécessaire à l'obtention de cette puissance.

Les calculs de puissance en statistique se font généralement avant que l'expérience ne soit menée. On s'en sert principalement pour estimer le nombre d'observations nécessaire pour que l'expérience ait la qualité statistique requise.

Le modèle de Cox exprime le risque instantané de survenue de l'événement λ_(t,X) sous la forme : λ_(t,X) = λ_0(t) exp(β₁X₁ + … + β_pX_p).

Cette formule appelle quelques commentaires. Le risque instantané se décompose en 2 termes dont l'un dépend du temps t et l'autre des variables X_j. Si par exemple, les variables X_j représentent des facteurs de risque et si elles sont toutes égales à 0, λ_0(t) est le risque instantané de sujets ne présentant aucun facteur de risque. La forme de λ_0(t) n'étant pas précisée, c'est plutôt l'association entre les variables X_j et la survenue de l'événement considéré qui est l'intérêt central du modèle. Cela revient à déterminer les coefficients β_j.

XLSTAT permet donc de tester si le coefficient β₁ du modèle de Cox est différent de 0. Si β₁ ≠ 0, alors on pourra dire que le facteur testé est un facteur de risque. Pour plus de détails sur ce modèle, voir le chapitre sur ce sujet. Nous allons donc tester l'hypothèse :

• H₀ : β₁ = 0
• H_a : β₁ ≠ 0

Pour cela, nous utiliserons la statistique de Wald : La puissance du test est calculée à l'aide d'une approximation et dépend de la loi normale, de la proportion d'individus qui ne sont pas censurés, de la variance de la variable X₁, de la valeur supposée de β₁ notée B et du R² obtenu par la régression des autres variables explicatives du modèle sur la variable X₁. On obtient alors la puissance de ce test.

Calcul de la taille de l'échantillon pour le modèle de Cox en prenant en compte la puissance statistique

Afin de calculer le nombre d'observations nécessaires, XLSTAT utilise un algorithme de recherche de racine d'une fonction appelé algorithme Van Wijngaarden-Dekker-Brent (Brent, 1973). Cet algorithme est adapté au cas où les dérivées de la fonction ne sont pas connues. On cherche ainsi N tel que

puissance_test(N)-puissance_recherchée=0

On obtient donc la taille N telle que la puissance soit la plus proche possible de la puissance recherchée.

Calcul de B

Le coefficient B(Log(Rapport de risque)) est l'estimation du coefficient β₁ tel qu'il apparaît dans l'équation suivante : log(λ_(t,X) / λ_0(t)) = β₁X₁ + … + β_kX_k

β₁ représente le changement du logarithme du rapport de risque lorsque X₁ augmente de 1 (toutes les autres variables restant constantes). Si on préfère partir du rapport de risque on prendra une valeur que l'on transformera en son logarithme. Ainsi pour un rapport de risque de 2, on aura B=ln(2)=0,693.