Comparaison de méthodes

Lors de la mise au point d'une nouvelle méthode pour mesurer la concentration ou la quantité d'un élément (molécule, microorganisme, ...), vous pouvez vouloir vérifier si elle donne des résultats similaires à une méthode de référence ou à méthode comparable. S'il y a une différence, il peut être intéressant de savoir si cela est dû à un biais qui dépend ou non de l'endroit où l'on se trouve sur l'échelle de variation. Si une nouvelle méthode de mesure est moins chère qu'une méthode standard et que vous savez qu'il existe un biais, il est possible de prendre en compte ce dernier pour corriger les résultats obtenus.

XLSTAT offre une série d'outils pour évaluer la performance d'une méthode par rapport à une autre.

Test t de Student sur données appariées

XLSTAT propose parmi les méthodes de comparaison, le test t de Student sur données appariées. Ce test permet de tester l'hypothèse H0 que la moyenne des différences entre les deux méthodes n'est pas différente de 0, contre l'hypothèse alternative Ha qu'elle l'est.

Nuages de points pour la comparaison de méthode

Dans un premier temps, XLSTAT affiche un nuage de points pour comparer la nouvelle méthode à une méthode de référence. Si les données sont réparties des deux côtés de la bissectrice (qui correspond à une identité parfaite des méthodes) tout en en étant proche, les deux méthodes donnent des résultats cohérents et proches. Si les données sont au-dessus de la ligne, la nouvelle méthode surestime la quantité mesurée. Si les données sont sous la ligne, la nouvelle méthode sous-estime la quantité mesurée, au moins par rapport à la méthode avec laquelle la comparaison est effectuée. Si les données croisent la bissectrice, le biais dépend de là où l'on se trouve sur l'échelle de variation. Si les données sont dispersées de façon aléatoire autour de la bissectrice avec des observations loin d'elle, la nouvelle méthode n'est pas performante.

Biais entre deux méthodes

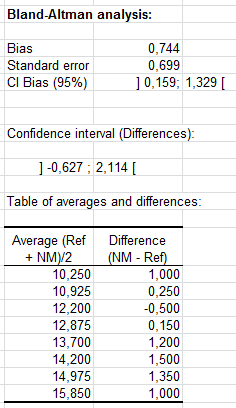
Le biais est estimé par la moyenne des différences entre les deux méthodes. Si des répétitions sont disponibles, dans un premier temps on calcule la moyenne des répétitions. L'écart-type du biais est calculé, ainsi qu'un intervalle de confiance. Idéalement, cet intervalle de confiance doit comprendre la valeur 0.

Remarque : Le biais est calculé pour le critère qui a été choisi pour l'analyse de Bland Altman (différence, différence en % ou ratio).

Analyse de Bland Altman et méthodes de comparaison liées

Bland et Altman recommandent de représenter la différence (T-S) entre la méthode en cours d'évaluation (T) et une méthode de référence ou comparable (S) en fonction de la moyenne (T+S)/2 des résultats obtenus pour les deux méthodes. Dans le cas idéal, il ne devrait y avoir aucune corrélation en la différence et la moyenne, qu'il y ait un biais ou non. XLSTAT teste si la corrélation est significativement différente de 0 ou non. Plusieurs possibilités sont proposées pour les ordonnées du graphique : vous pouvez choisir la différence (T-S), la différence en % de la somme 100*(T-S)/(T+S), et le ratio (T/S). Sur le graphique de Bland Altman, XLSTAT affiche la ligne correspondent au biais, les intervalles de confiance autour du biais, et des différences (ou de la différence en % ou du ratio).

Histogramme et box plot pour la comparaison de méthode

L'histogramme et le box plot des différences (ou différences en % ou ratio) sont affichés pour valider l'hypothèse que cette quantité est distribuée suivant une loi normale, sachant que cette hypothèse est utilisée pour calculer les intervalles de confiance autour du biais et des différences individuelles. Lorsque l'échantillon est de petite taille, l'histogramme est de peu d'intérêt et il faut seulement considérer le box plot. Si la distribution ne semble pas normale, on peut vérifier ce point avec un test de normalité, et les intervalles de confiance doivent être considérés avec prudence.