Linear regression
Use this tool to create a simple or multiple linear regression model for explanation or prediction. Available in Excel using the XLSTAT software.
What is linear regression analysis?
Linear regression is undoubtedly one of the most frequently used statistical modeling methods. A distinction is usually made between simple regression(with only one explanatory variable) and multiple regression (several explanatory variables) although the overall concept and calculation methods are identical.
The principle of linear regression is to model a quantitative dependent variable Y through a linear combination of p quantitative explanatory variables, X1, X2, …, Xp. The linear regression equation is written for observation i as follows:
yi = a1x1i + a2x2i + ... + apxpi + ei
where yi is the value observed for the dependent variable for observation i, xki is the value taken by variable k for observation i, and ei is the error of the model.
Since the model is found by using the ordinary least squares (OLS) method (the sum of squared errors ei² is minimized), many wonder: is OLS the same as linear regression? Not really, OLS is simply the name of the method that enables us to find the regression line equation.
The linear regression hypotheses are that the errors ei follow the same normal distribution N(0,s) and are independent.
Going further: variable selection in linear regression
Not all variables are important or significant in the linear regression model. It is possible to select only the most important ones using one of the four methods available in XLSTAT:
- Best model: This method allows you to select the best mode among all the models that can handle a number of variables varying from "Min variables" to "Max Variables". Furthermore, the user can choose several "criteria" to determine the best model: Adjusted R², Mean Square of Errors (MSE), Mallows Cp, Akaike's AIC, Schwarz's SBC, Amemiya's PC.
- Stepwise: The selection process starts by adding the variable with the largest contribution to the model (the criterion used is Student's t statistic). If a second variable is such that the probability associated with its t is less than the "Probability for entry", it is added to the model. The same is true for a third variable. After the third variable is added, the impact of removing each variable that is present in the model after it has been added is evaluated (still using the t statistic). If the probability is greater than the "Probability of removal", the variable is removed. The procedure continues until no more variables can be added or removed.
- Forward: The procedure is the same as for stepwise selection, except that variables are only added and never removed.
- Backward: The procedure starts by simultaneously adding all variables. The variables are then removed from the model using the same procedure as for stepwise selection.
How to validate linear regression assumptions?
One must verify two main assumptions for linear regression regarding the residuals:
- they must follow a normal distribution
- they must be independent
Use the various tests displayed in the linear regression results to check retrospectively that the underlying hypotheses have been correctly verified.
The normality of the residuals can be checked by analyzing certain charts or by running a Shapiro-Wilk test on the residuals. To do this, you need to activate the respective test in the Test assumptions sub-tab. The independence of the residuals can be checked by analyzing certain charts or by using the Durbin-Watson test (under the Time Series menu).
How to correct Heteroscedasticity and Autocorrelation?
As mentioned earlier, homoscedasticity and independence of the error terms are key hypotheses in linear regression, where it is assumed that the variances of the error terms are independent and identically distributed and normally distributed.
XLSTAT allows correcting for heteroscedasticity and autocorrelation, which can can occur with different methods, such as the estimator suggested by Newey and West (1987).
What results for linear regression can I see in XLSTAT?
- Summary of variable selection: When a selection method has been chosen, XLSTAT displays the selection summary. For a stepwise selection, the statistics corresponding to the different steps are displayed. Where the best model for a number of variables varying from p to q has been selected, the best model for each number of variables is displayed with the corresponding statistics and the best model for the chosen criterion is displayed in bold.
- Goodness of fit statistics: The statistics related to the fitting of the regression model are displayed in this table:
- Observations: the number of observations used in the calculations. In the formulas shown below, n is the number of observations.
- Sum of weights: the sum of the weights of the observations used in the calculations. In the formulas shown below, W is the sum of the weights.
- DF: the number of degrees of freedom for the chosen model (corresponding to the error part).
- R²: the determination coefficient for the model. This coefficient, whose value is between 0 and 1, is only displayed if the constant of the model has not been set by the user. The R² is interpreted as the proportion of the variability of the dependent variable that is explained by the model. The closer R² is to 1, the better the model is. The problem with the R² is that it does not take into account the number of variables used to fit the model.
- Adjusted R²: the adjusted determination coefficient for the model. The adjusted R² can be negative if the R² is near to zero. This coefficient is only calculated if the constant of the model has not been set by the user. The adjusted R² is a correction to the R² which takes into account the number of variables used in the model.
- MSE: the mean of the squares of the errors (MSE).
- RMSE: the root mean square of the errors (RMSE) is the square root of the MSE.
- MAPE: the Mean Absolute Percentage Error.
- DW: the Durbin-Watson statistic. This coefficient is the first order autocorrelation coefficient and is used to check that the residuals of the model are not autocorrelated, given that the independence of the residuals is one of the basic hypotheses of linear regression. The user can refer to a table of Durbin-Watson statistics to verify if the independence hypothesis for the residuals is acceptable.
- Cp: Mallows Cp coefficient. The nearer the Cp coefficient is to p*, the less the model is biased.
- AIC: Akaike’s Information Criterion. This criterion, proposed by Akaike (1973) is derived from the information theory and uses Kullback and Leibler's measurement (1951). It is a model selection criterion that penalizes models where the addition of new explanatory variables does not provide sufficient information to the model, the information being measured through the MSE. The aim is to minimize the AIC criterion.
- SBC: Schwarz’s Bayesian Criterion. This criterion, proposed by Schwarz (1978) is similar to the AIC, and the aim is to minimize it.
- PC: Amemiya’s Prediction Criterion. This criterion, proposed by Amemiya (1980) is used, like the adjusted R² to take account of the parsimony of the model.
- Press RMSE: Press' statistic is only displayed if the corresponding option has been activated in the dialog box. Press's RMSE can then be compared to the RMSE. A large difference between the two indicates that the model is sensitive to the presence or absence of certain observations in the model.
- Type I SS table: it is used to visualize the influence that progressively adding explanatory variables has on the fitting of the model, as regards the sum of the squares of the errors (SSE), the mean of the squares of the errors (MSE), Fisher's F, or the probability associated with Fisher's F. The lower the probability, the larger the contribution of the variable to the model, all the other variables already being in the model. The sums of squares in the Type I table always add up to the model SS. Note: the order in which the variables are selected in the model influences the values obtained.
- Type III SS table: it is used to visualize the influence that removing an explanatory variable has on the fitting of the model, all other variables being retained, as regards the sum of the squares of the errors (SSE), the mean of the squares of the errors (MSE), Fisher's F, or the probability associated with Fisher's F. The lower the probability, the larger the contribution of the variable to the model, all the other variables already being in the model. Note: unlike Type I SS, the order in which the variables are selected in the model has no influence on the values obtained.
- Analysis of variance table: it is used to evaluate the explanatory power of the explanatory variables. Where the constant of the model is not set to a given value, the explanatory power is evaluated by comparing the fit (as regards least squares) of the final model with the fit of the rudimentary model including only a constant equal to the mean of the dependent variable. Where the constant of the model is set, the comparison is made with respect to the model for which the dependent variable is equal to the constant which has been set.
- The parameters of the model table: it displays the estimate of the parameters, the corresponding standard error, the Student’s t, the corresponding probability, as well as the confidence interval.
- Model equation: the equation of the model is then displayed to make it easier to read or re-use the model.
- Standardized coefficients table: the table of standardized coefficients is used to compare the relative weights of the variables. The higher the absolute value of a coefficient, the more important the weight of the corresponding variable. When the confidence interval around standardized coefficients has value 0 (this can be easily seen on the chart of normalized coefficients), the weight of a variable in the model is not significant.
- Predictions and residuals table: the predictions and residuals table indicates, for each observation, its weight, the value of the qualitative explanatory variable, if there is only one, the observed value of the dependent variable, the model's prediction, the residuals, the confidence intervals together with the adjusted prediction if the corresponding options have been activated in the dialog box. Two types of confidence interval are displayed: a confidence interval around the mean (corresponding to the case where the prediction would be made for an infinite number of observations with a set of given values for the explanatory variables) and an interval around the isolated prediction (corresponding to the case of an isolated prediction for the values given for the explanatory variables). The second interval is always greater than the first, the uncertainty being larger. If validation data have been selected, they are displayed at the end of the table.
- The table of influence diagnostics displays for each observation, its weight, the corresponding residual, the standardized residual (divided by the RMSERMSE), the studentized residual, the deleted residual, the studentized deleted residual, the leverage, the Mahalanobis distance, the Cook's D, the CovRatio, the DFFit, the standardized DFFit, the DFBetas (one per model coefficient) and the standardized DFBetas.
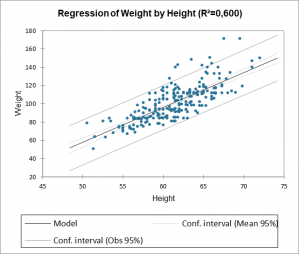
Finally, our XLSTAT software enables you to plot the regression line directly in Excel. You can monitor the linear regression error thanks to the confidence intervals that are also displayed in the chart at the beginning of this article.


analyze your data with xlstat
Related features