Cochran-Armitage trend test
The Cochran-Armitage trend test allows to check if a series of proportions vary linearly along a numeric variable. Do it in Excel using the XLSTAT software.
When to use a Cochran-Armitage trend test
The Cochran Armitage trend is used to test if a series of proportions, possibly computed from a contingency table, can be considered as varying linearly with an ordinal or continuous variable.
It can be a one- or two-sided test.
What is the Cochran-Armitage trend test
The Cochran-Armitage test allows to test if a series of proportions, can be considered as varying linearly with an ordinal or continuous score variable.
If X is the score variable, the statistic that is computed to test for the linearity is given by:
z = [Ʃi=1..r nr1(Xi - X)] / √ p+1 (1– p+1) s²
with s²=Ʃi=1..r ni+(Xi - X)²
Note: if X is an ordinal variable, the minimum value of X has no influence on the value of z.
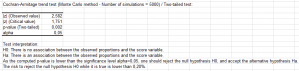
In the case of the two-tailed (or two-sided) test, the null (H0) and alternative (Ha) hypotheses are:
- H0: z = 0
- Ha: z ≠ 0
Note: z is asymptotically distributed as a standard Normal variable. Some statistical programs use z² to test the linearity. z² follows a Chi-square distribution with one degree of freedom.
In the one-tailed case, you need to distinguish the left-tailed (or lower-tailed or lower one-sided) test and the right-tailed (or upper-tailed or upper one-sided) test. In the left-tailed test, the following hypotheses are used:
- H0: z = 0
- Ha: z < 0
If Ha is chosen, one concludes that the proportions decrease when the score variable increases.
In the right-tailed test, the following hypotheses are used:
- H0: z = 0
- Ha: z > 0
If Ha is chosen, one concludes that the proportions increase when the score variable increases.

