Logistic regression (Binary, Ordinal, Multinomial, …)
Use logistic regression to model a binomial, multinomial or ordinal variable using quantitative and/or qualitative explanatory variables.
Definition of the logistic regression in XLSTAT
Principle of the logistic regression
Logistic regression is a frequently used method because it allows to model binomial (typically binary) variables, multinomial variables (qualitative variables with more than two categories) or ordinal (qualitative variables whose categories can be ordered). It is widely used in the medical field, in sociology, in epidemiology, in quantitative marketing (purchase or not of products or services following an action) and in finance for risk modeling (scoring).
The principle of the logistic regression model is to explain the occurrence or not of an event (the dependent variable noted Y) by the level of explanatory variables (noted X). For example, in the medical field, we seek to assess from what dose of a drug, a patient will be cured.
Models for logistic regression
Binomial logistic regression
Logistic and linear regression belong to the same family of models called GLM (Generalized Linear Model): in both cases, an event is linked to a linear combination of explanatory variables.
For linear regression, the dependent variable follows a normal distribution N(μ,σ) where μ is a linear function of the explanatory variables. For logistic regression, the dependent variable, also called the response variable, follows a Bernoulli distribution of parameter p (p is the mean probability that an event will occur) when the experiment is repeated once, or a Binomial(n,p) distribution if the experiment is repeated nn times (for example the same dose given to nn patients). The probability parameter p is here a function of a linear combination of explanatory variables.
The most common functions used to link probability p to the explanatory variables are the logistic function (we refer to the Logit model) and the standard normal distribution function (the Probit model). Both these functions are perfectly symmetric and sigmoid: XLSTAT provides two other functions: the complementary Log-log function which is closer to the upper asymptote, and the Gompertz function which, on the contrary, is closer the axis of abscissa.
In most software, the calculation of confidence intervals for the model parameters is as for linear regression assuming that the parameters are normally distributed. XLSTAT also offers the alternative "Likelihood ratio" method (Venzon and Moolgavkar, 1988). This method is more reliable as it does not require the assumption that the parameters are normally distributed. Being iterative, however, it can slow down the calculations.
Multinomial logistic regression
The principle of multinomial logistic regression is to explain or predict a variable that can take J alternative values (the J categories of the variable), as a function of explanatory variables. The binomial case seen previously is therefore a special case where J=2.
Within the framework of the multinomial model, a control category must be selected. Ideally, we will choose what corresponds to the "basic" or "classic" or "normal" situation. The estimated coefficients will be interpreted according to this control category. For ease of writing, the equations below are written considering the first category as the reference category.
The model proposed by XLSTAT to relate the probability of occurrence of an event to the explanatory variables is the logit model which is one of the four models proposed for the binomial case.
Contrary to linear regression, an exact analytical solution does not exist. XLSTAT uses the Newton-Raphson algorithm to iteratively find a solution.
Ordinal logistic regression
The principle of ordinal logistic regression is to explain or predict a variable that can take J ordered alternative values (only the order matters, not the differences), as a function of a linear combination of the explanatory variables. Binomial logistic regression is a special case of ordinal logistic regression, corresponding to the case where J=2.
XLSTAT makes it possible to use two alternative models to calculate the probabilities of assignment to the categories given the explanatory variables: the logit model and the probit model.
Unlike linear regression, an exact analytical solution does not exist. It is therefore necessary to use an iterative algorithm. XLSTAT uses a Newton-Raphson algorithm.
Results of the logistic regression in XLSTAT
XLSTAT displays a large number tables and charts to help in analyzing and interpreting the results.
Summary statistics: This table displays descriptive statistics for all the variables selected. For the quantitative variables, the number of missing values, the number of non-missing values, the mean and the standard deviation (unbiased) are displayed. For qualitative variables, including the dependent variable, the categories with their respective frequencies and percentages are displayed.
Correlation matrix: This table displays the correlations between the explanatory variables. Note that if the dependent variable is binary, the biserial correlation coefficient is used to calculate the correlation between the quantitative explanatory variables and the dependent variable.
Summary of the variables selection: Where a selection method has been chosen, XLSTAT displays the selection summary. For a stepwise selection, the statistics corresponding to the different steps are displayed. Where the number of variables varies from p to q, the best model for each number or variables is displayed with the corresponding statistics and the best model for the criterion chosen is displayed in bold.
Goodness of fit coefficients: This table displays a series of statistics for the independent model (corresponding to the case where the linear combination of explanatory variables reduces to a constant) and for the adjusted model.
Observations: The total number of observations taken into account (sum of the weights of the observations);
Sum of weights: The total number of observations taken into account (sum of the weights of the observations multiplied by the weights in the regression);
DF: Degrees of freedom;
-2 Log(Like.): The logarithm of the likelihood function associated with the model;
R² (McFadden): Coefficient, like the R², between 0 and 1 which measures how well the model is adjusted. This coefficient is equal to 1 minus the ratio of the likelihood of the adjusted model to the likelihood of the independent model;
R²(Cox and Snell): Coefficient, like the R², between 0 and 1 which measures how well the model is adjusted. This coefficient is equal to 1 minus the ratio of the likelihood of the adjusted model to the likelihood of the independent model raised to the power 2/Sw, where Sw is the sum of weights.
R²(Nagelkerke): Coefficient, like the R², between 0 and 1 which measures how well the model is adjusted. This coefficient is equal to ratio of the R² of Cox and Snell, divided by 1 minus the likelihood of the independent model raised to the power 2/Sw;
AIC: Akaike’s Information Criterion;
SBC: Schwarz’s Bayesian Criterion.
Iterations: Number of iterations before convergence.
Test of the null hypothesis H0: Y=p0: The H0 hypothesis corresponds to the independent model which gives probability p0 whatever the values of the explanatory variables. We seek to check if the adjusted model is significantly more powerful than this model. Three tests are available: the likelihood ratio test (-2 Log(Like.)), the Score test and the Wald test. The three statistics follow a chi2 distribution whose degrees of freedom are shown.
Type II analysis: This table is only useful if there is more than one explanatory variable. Here, the adjusted model is tested against a test model where the variable in the row of the table in question has been removed. If the probability Pr>LR is less than a significance threshold which has been set (typically 0.05), then the contribution of the variable to the adjustment of the model is significant. Otherwise, it can be removed from the model.
Model parameters:
Binary case: The parameter estimate, corresponding standard deviation, Wald's chi2, the corresponding p-value and the confidence interval are displayed for the constant and each variable of the model. If the corresponding option has been activated, the "profile likelihood " intervals are also displayed.
Multinomial case: In the multinomial case, (J-1)*(q+1) parameters are obtained, where J is the number of categories and q is the number of variables in the model. Thus, for each explanatory variable and for each category of the response variable (except for the reference category), the parameter estimate, corresponding standard deviation, Wald's chi2, the corresponding p-value and the confidence interval are displayed. The odds-ratios with corresponding confidence interval are also displayed.
Ordinal case: In the ordinal case, (J-1)+q parameters are obtained, where J is the number of categories and p is the number of variables in the model. Thus, for each explanatory variable and for each category of the response variable, the parameter estimate, corresponding standard deviation, Wald's chi2, the corresponding p-value and the confidence interval are displayed.
The equations of the model are then displayed to make it easier to read or re-use the model.
The table of standardized coefficients (also called beta coefficients) are used to compare the relative weights of the variables. The higher the absolute value of a coefficient, the more important the weight of the corresponding variable. When the confidence interval around standardized coefficients has value 0 (this can easily be seen on the chart of standardized coefficients), the weight of a variable in the model is not significant.
When requested, the covariance matrix of the parameters is then displayed.
The marginal effects at the point corresponding to the means of the explanatory variables are then displayed. The marginal effects are mainly of interest when compared to each other. By comparing them, one can measure the relative impact of each variable at the given point. The impact can be interpreted as the influence of a small variation of each explanatory variable, on the dependent variable. A confidence interval calculated using the Delta method is displayed. XLSTAT provides these results for both quantitative and qualitative variables, whether simple factors or interactions. For qualitative variables, the marginal effect indicates the impact of a change in category (from the first category to the category of interest).
The predictions and residuals table shows, for each observation, its weight, the value of the quantitative explanatory variable (if there is only one), the observed value of the dependent variable, the model's prediction, the same values divided by the weights (for the sum(binary) case), the probabilities for each category of the dependent variable, and the confidence intervals (in the binomial case).
The influence diagnostics table makes it possible to assess the impact of each observation on the quality of the model or on the value of the coefficients of the model. It is only displayed in the binomial and multinomial cases.
This classification table displays the table showing the number of well-classified and miss-classified observations for both categories. The sensitivity, specificity and the overall percentage of well-classified observations are also displayed. If a validation sample has been extracted, this table is also displayed for the validation data.
ROC curve: The ROC curve is used to evaluate the performance of the model by means of the area under the curve (AUC) and to compare several models together.
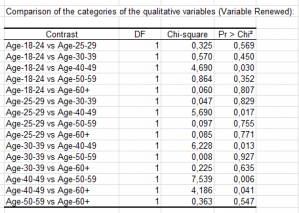
Comparison of the categories of the qualitative variables: If one or more explanatory qualitative variables have been selected, the results of the equality tests for the parameters taken in pairs from the different qualitative variable categories are displayed.
If only one quantitative variable has been selected, the probability analysis table allows to see to which value of the explanatory variable corresponds a given probability of success.


analyze your data with xlstat
Related features