ANCOVA (Analysis of Covariance)
ANCOVA (Analysis of Covariance) is a model that holds both qualitative & quantitative independent variables. Do it in Excel with the XLSTAT software.
What is ANCOVA (Analysis of Covariance)
ANCOVA (ANalysis of COVAriance) can be seen as a mix of ANOVA and linear regression as the dependent variable is of the same type, the model is linear and the hypotheses are identical. In reality it is more correct to consider ANOVA and linear regression as special cases of ANCOVA.
The ANCOVA model
If p is the number of quantitative variables, and q the number of factors (the qualitative variables including the interactions between qualitative variables), the ANCOVA model is written as follows:
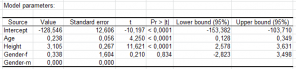
yi = β0 + ∑j=1...p βjxij + ∑j=1...q βk(i,j),j + εi
where yi is the value observed for the dependent variable for observation i, xij is the value taken by quantitative variable j for observation i, k(i,j) is the index of the category of factor j for observation i and εi is the error of the model.
The hypotheses used in ANOVA are identical to those used in linear regression and ANOVA: the errors εi follow the same normal distribution N(0,s) and are independent.
Interactions in ANCOVA
XLSTAT enables you to perform one and multiple way ANCOVA up to order 4 interactions between factors can be included in the model. One of the features of ANCOVA is to enable interactions between quantitative variables and factors to be taken into account. The main application is to test if the level of a factor (a qualitative variable) has an influence on the coefficient (often called slope in this context) of a quantitative variable. Comparison tests are used to test if the slopes corresponding to the various levels of a factor differ significantly or not.
Results for an Analysis of Covariance in XLSTAT
The results contain residuals analysis, Type I SS, Type III SS, and predictions.
Several multiple comparison methods can optionally be performed: Bonferroni's and Dunn-Sidak corrected t test, Tukey's HSD test, Fisher's LSD test, Duncan's test, Newman-Keuls' (SNK) method and the REGWQ method.
The Dunnett's test is available to allow users to perform multiple comparisons with control (MCC) and Multiple comparison with the best (MCB).


analyze your data with xlstat
Related features