Mantel test

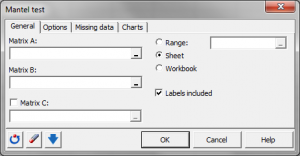
What is the Mantel test

The Mantel test measures and tests the linear correlation between two proximity matrices (simple Mantel test) or between two matrices while taking into account the linear correlation with a third matrix (partial Mantel test).

Simple Mantel test

Mantel proposed a first statistic to measure the correlation between two proximity (similarity or dissimilarity) and symmetric A and B matrices of size n:

Z(AB) = ∑_(i-n...n-1) ∑_(j-i+1...n) a_ij b_ij

In the case where the matrices are not symmetric, the computations are possible.

While it is not a problem to compute the correlation coefficient between two sets of proximity coefficients, testing their significance cannot be done using the usual approach that is used to test correlations: to use the latter tests, one needs to assume the independence of the data, which is not the case here. A permutation test has been proposed to determine if the correlation coefficient can be considered as showing a significant correlation between the matrices or not. It can be one- or two-sided.

The Mantel test consists of computing the correlation coefficient that would be obtained after permuting the rows and columns of one of the matrices. The p-value is calculated using the distribution of the r(AB) coefficients obtained from S permutations. In the case where n, the number of rows and columns of the matrices, is lower than 10, all the possible permutations can easily be computed. If n is greater than 10, one needs to randomly generate a set of S permutations in order to estimate the distribution of r(AB).

Partial Mantel test

A Mantel test for more than two matrices has been proposed: when we have three proximity matrices A, B and C, the partial Mantel statistic r(AB.C) for the A and B matrices knowing the C matrix is computed as a partial correlation coefficient. In order to determine if the coefficient is significantly different from 0, a p-value is computed using random permutations.