k-means clustering
k-means clustering is a popular aggregation (or clustering) method. Run k-means on your data in Excel using the XLSTAT add-on statistical software.
Description of the k-means clustering analysis in XLSTAT
General description
k-means clustering was introduced by McQueen in 1967. Other similar algorithms had been developed by Forgey (1965) (moving centers) and Friedman (1967).
k-means clustering has the following advantages:
- An object may be assigned to a class during one iteration then change class in the following iteration, which is not possible with Agglomerative Hierarchical Clustering, where assignment is irreversible.
- By multiplying the starting points and the repetitions, several solutions may be explored.
The disadvantage of this method is that it does not give a consistent number of classes or enable the proximity between classes or objects to be determined.
The k-means and AHC methods are therefore complementary.
Note: if you want to take qualitative variables into account in the clustering, you must first perform a Multiple Correspondence Analysis (MCA) and consider the resulting coordinates of the observations on the factorial axes as new variables.
Principle of the k-means method
k-means clustering is an iterative method which, wherever it starts from, converges on a solution. The solution obtained is not necessarily the same for all starting points. For this reason, the calculations are generally repeated several times in order to choose the optimal solution for the selected criterion.
For the first iteration, a starting point is chosen which consists of associating the center of the k classes with k objects (either taken at random or not). Afterwards, the distance between the objects and the k centers are calculated, and the objects are assigned to the centers they are nearest to. Then the centers are redefined from the objects assigned to the various classes. The objects are then reassigned depending on their distances from the new centers. And so on until convergence is reached.
Classification criteria for k-means Clustering
Several classification criteria may be used to reach a solution. XLSTAT offers four criteria for the k-means minimization algorithm:
Trace(W): The W trace, pooled SSCP matrix, is the most traditional criterion. Minimizing the W trace for a given number of classes amounts to minimizing the total within-class variance — in other words, minimizing the heterogeneity of the groups. This criterion is sensitive to effects of scale. In order to avoid giving more weight to certain variables and not to others, the data must be normalized beforehand. Moreover, this criterion tends to produce classes of the same size.
Determinant(W): The determinant of W, pooled within covariance matrix, is a criterion considerably less sensitive to effects of scale than the W trace criterion. Furthermore, group sizes may be less homogeneous than with the trace criterion.
Wilks lambda: The results given by minimizing this criterion are identical to that given by the determinant of W. Wilks’ lambda criterion corresponds to the division of determinant(W) by determinant(T) where T is the total inertia matrix. Dividing by the determinant of T always gives a criterion between 0 and 1.
Trace(W) / Median: If this criterion is chosen, the class centroid is not the mean point of the class but the median point, which corresponds to an object of the class. The use of this criterion gives rise to longer calculations.
Results for k-means clustering in XLSTAT
Summary statistics: This table displays the descriptors of the objects, the number of observations, the number of missing values, the number of non-missing values, the mean and the standard deviation.
Correlation matrix: This table is displayed to give you a view of the correlations between the various variables selected.
Evolution of the within-class inertia: If you have selected a number of classes between two bounds, XLSTAT displays at first the evolution of the within-class inertia, which reduces mathematically when the number of classes increases. If the data is distributed homogeneously, the decrease is linear. If there is actually a group structure, an elbow is observed for the relevant number of classes.
Evolution of the silhouette score: If you have selected a number of classes between two bounds, a table with its associated chart shows the evolution of the silhouette score for each k. The optimal number of classes is the k whose silhouette score is closest to 1.
Optimization summary: This table shows the evolution of the within-class variance. If several repetitions have been requested, the results for each repetition are displayed. The repetition giving the best classification is displayed in bold.
Statistics for each iteration: This table shows the evolution of miscellaneous statistics calculated as the iterations for the repetition proceed, given the optimum result for the chosen criterion. If the corresponding option is activated in the Charts tab, a chart showing the evolution of the chosen criterion as the iterations proceed is displayed.
Note: if the values are standardized (option in the Options tab), the results for the optimization summary and the statistics for each iteration are calculated in the standardized space. On the other hand, the following results are displayed in the original space if the "Results in the original space" option is activated.
Inertia decomposition for the optimal classification: This table shows the within-class inertia, the between-class inertia and the total inertia.
Initial class centroids: This table shows the initial class centroids computed thanks to the initial random partition or with K|| and K++ algorithms. In case you defined the centers, this table shows the selected class centroids.
Class centroids: This table shows the class centroids for the various descriptors.
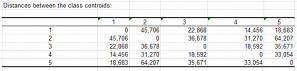
Distance between the class centroids: This table shows the Euclidean distances between the class centroids for the various descriptors.
Central objects: This table shows the coordinates of the nearest object to the centroid for each class.
Distance between the central objects: This table shows the Euclidean distances between the class central objects for the various descriptors.
Results by class: The descriptive statistics for the classes (number of objects, sum of weights, within-class variance, minimum distance to the centroid, maximum distance to the centroid, mean distance to the centroid) are displayed in the first part of the table. The second part shows the objects.
Results by object: This table shows the assignment class for each object in the initial object order.
- Distance to centroid: this column shows the distance between an object and its class centroids.
- Correlations with centroids: this column shows the Pearson correlation between an object and its class centroids.
- Silhouette scores: this column shows the silhouette score of each object.
Silhouette scores (Mean by class): This table and its graph are displayed and show the mean silhouette score of each class and the silhouette score for the optimal classification (mean of means by class).
Contribution (Analysis of variance) : This table indicates the variables that contribute the most to the separation of the classes by performing an ANOVA.
Profile plot: This chart allows you to compare the means of the different classes that have been created.


analyze your data with xlstat
Related features