Two-sample comparison of variances
2-sample comparison of variance tests including Fisher's test compare the variances of 2 samples. Run them in Excel with the XLSTAT statistical software.
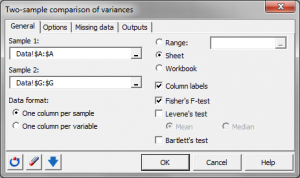
What is a two-sample comparison of variances test
Take a sample S1 comprising n1 observations with variance s1². Take a second sample S2 comprising n2 observations with variance s2². Two-sample variance tests allow to check if one variance is significantly different from the second. XLSTAT offers three tests for comparing the variances of the two samples.
Two-sample comparison of variances tests in XLSTAT
Three parametric tests are offered for the comparison of the variances of two independent samples.
Fisher's F-test
Let R be the assumed ratio of the variances (R is 1 when equality is assumed).
The test statistic F is given by:
F = s1² ⁄ R*s2²
This statistic follows a Fisher distribution with (n1-1) and (n2-1) degrees of freedom if both samples follow a normal distribution.
Three types of test are possible depending on the alternative hypothesis chosen:
- two-tailed test,
- left-tailed test,
- right-tailed test.
Levene's test
Levene's test can be used to compare two or more variances. It is a two-tailed test with the following hypotheses:
- H0 : s1² = s2²
- Ha : s1² ≠ s2²
The statistic from this test is more complex than that from the Fisher test and involves absolute deviations at the mean or at the median. The use of the mean is recommended for symmetrical distributions with averagely thick tails. The use of the median is recommended for asymmetric distributions. The Levene statistic follows a Fisher’s F distribution with 1 and n1+n2-2 degrees of freedom.
Bartlett’s homogeneity of variances test
Bartlett's test can be used to compare two or more variances. This test is sensitive to the normality of the data. In other words, if the hypothesis of normality of the data seems fragile, it is better to use Levene's or Fisher's test. On the other hand, Bartlett's test is more powerful if the samples follow a normal distribution.
This is also a two-tailed test similar to the Levene's test. Bartlett's statistic follows a Chi-square distribution with one degree of freedom.

