Time series descriptive statistics
Several time series descriptive statistics including autocorrelation check & white noise tests are available in Excel using the XLSTAT statistical software.
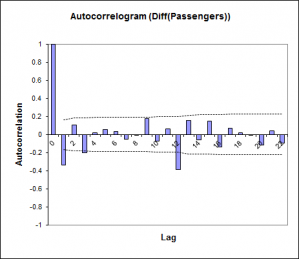
One of the key issues in time series analysis is to determine whether the value we observe at time t depends on what has been observed in the past or not. If the answer is yes, then the next question is how.
Autocovariances, autocorrelations, and partial autocorrelations
The sample autocovariance function (ACVF) and the autocorrelation function (ACF) give an idea of the degree of dependence between the values of a time series. The visualization of the ACF or of the partial autocorrelation function (PACF) helps to identify the suitable models to explain the past observations and to do predictions. The theory shows that the PACF function of an AR(p) – an autoregressive process of order p - is zero for lags greater than p.
Cross-correlations
The cross-correlations function (CCF) allows to relate two time series, and to determine if they co-vary and to which extend. The ACVF, the ACF, the PACF and CCF are computed by this tool.
Normality and white noise tests at different time lags
One important step in time series analysis is the transformation of time which goal is to obtain a white noise. Obtaining a white noise means that all deterministic and autocorrelations components have been removed. Several white noise tests, based on the ACF, are available to test whether a time series can be assumed to be a white noise or not.

