Spectral analysis
Spectral analysis investigates the distribution of frequency components of a time series. Available in Excel using the XLSTAT add-on statistical software.
Spectral analysis
Spectral analysis is a powerful time series analysis method that lets you describe your data that is in the time domain, in the frequency domain.
XLSTAT provides a complete Spectral analysis feature, which enables several options that will let you gain a deep insight on your data:
- Test if your time series (signal) is a white noise
- Estimate the spectral density by choosing one of several kernel types
- Calculate the cross spectrum (quadrature spectrum, ...)
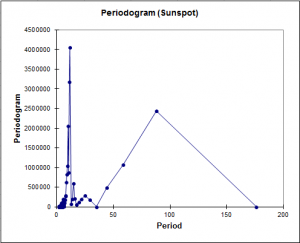
- Display the spectral density and the periodogram
- Select date data and run the analysis for one to several time series
What is the use of spectral analysis?
Spectral analysis allows transforming a time series (time signal) into its coordinates in the space of frequencies, and then to analyze its characteristics in this space. The magnitude and phase can be extracted from the coordinates. It is then possible to build representations such as the periodogram or the spectral density, and to test if the series is stationary. By studying the spectral density, seasonal components and/or noise can be identified. Spectral analysis is a very general method used in a variety of domains.
The spectral representation of a time series Xt, (t=1,…,n), decomposes Xt into a sum of sinusoidal components with uncorrelated random coefficients. From there we can obtain decomposition the autocovariance and autocorrelation functions into sinusoids.
Spectral density
The spectral density is a function that can be interpreted as the covariance of the time signal. This function corresponds to the transform of a continuous time series. However, we usually have only access to a limited number of equally spaced data, and therefore, we need to obtain first the discrete Fourier coordinates (cosine and sine transforms), and then the periodogram. From the periodogram, using a smoothing function, we can obtain a spectral density estimate which is a better estimator of the spectrum.
The spectral density estimate (or discrete spectral average estimator) of the time series Xt uses weights. The weights, are either fixed by the user, or determined by the choice of a kernel. XLSTAT suggests the use of the following kernels:
- Parzen
- Quadratic spectral
- Tukey-Hanning
- Truncated
White noise tests
XLSTAT optionally displays two test statistics and the corresponding p-values for white noise: Fisher's Kappa and Bartlett's Kolmogorov-Smirnov statistic.
Spectral analysis in XLSTAT
Using fast and powerful methods, XLSTAT automatically computes the Fourier cosine transform and sine transform of Xt, for each Fourier frequency, and then the various functions that derive from these transforms.
Tutorial on how to run a spectral analysis in Excel using the XLSTAT software
Here is an example on how to run a spectral analysis with XLSTAT


analyze your data with xlstat
Related features