Non parametric tests on two independent samples
The non-parametric Mann-Whitney test compares the ranks of two independent samples. Run it in Excel with the XLSTAT statistical add-on software.
What are non-parametric tests for two independent samples?
Non-parametric tests are not based on statistical distributions. Therefore, they can be used even if the validity conditions of parametric tests are not checked. Nonparametric tests on two independent samples are used to compare the distribution of two independent samples. If you want to learn more about the difference between parametric and non-parametric tests, read our article on this topic.
As for non-parametric tests, a distinction is made between independent samples (e.g. comparing annual sales of a supermarket chain between two regions) and paired samples (e.g. comparing annual sales within the same region over two years). The Mann-Withney test can be used for independent samples, while the sign and Wilcoxon signed-rank tests can be used if you have paired samples.
Please consult our guide if you do not know which statistical test to choose.
What is a Mann-Whitney test?
Three researchers, Mann, Whitney, and Wilcoxon, independently developed a very similar nonparametric test to determine whether samples come from a single population or from two different populations, meaning that the two samples can be considered identical or not based on their ranks. This test is often called the Mann-Whitney test, sometimes also the Wilcoxon-Mann-Whitney test or the Wilcoxon Rank-Sum test. XLSTAT can perform a two-tailed or a one-tailed test.
If we denote D as the assumed difference in position between the samples (in general, we test for equality, and D is therefore 0) and P1-P2 as the difference in position between the samples, three tests are possible, depending on the alternative hypothesis chosen:
- the two-tailed test: H0: P1 - P2 = D and Ha: P1 - P2 ≠ D
- the left-tailed test: H0: P1 - P2 = D and Ha: P1 - P2 < D
- the right-tailed test: H0: P1 - P2 = D and Ha: P1 - P2 > D
Let S1 be a sample consisting of n1 observations (x1, x2, ..., xn1), and S2 be a second sample consisting of n2 observations (y1, y2, ..., yn2) and independent of S1. Let N be the sum of n1 and n2.
XLSTAT computes the Wilcoxon Ws statistic, which measures the difference in position between the first sample S1 and the sample S2 from which D was subtracted. We combine the values obtained for both samples and then rank them. For XLSTAT, the Ws statistic is the sum of the ranks of the first samples.
Thus, for the expected value and the variance of Ws, the following holds:
E(Ws) = 1/2 n1(N + 1) and V(Ws) = 1/12 n1n2(N + 1)
The Mann-Whitney U statistic is the sum of the number of pairs (xi, yi) where xi>yi, among all possible pairs. We show that:
E(U) = n1n2/2 and V(U) = 1/12 n1n2(N + 1)
We can conclude that the variances of Ws and U are identical. In fact, the relationship between U and Ws is:
Ws = U + n1(n1 + 1) / 2
What are the options for the Mann-Whitney test in XLSTAT?
XLSTAT offers several options in the dialog box of the Mann-Whitney test. Here is a description:
Data / Sample 1: Select a column of data corresponding to the first sample.
Sample identifiers / Sample 2: Select a column of data corresponding to the second sample.
Data Format: Check the One column per sample option and select one column (row in row mode) per sample.
Column/Row labels: Activate this option if the first row (column mode) or first column (rows mode) of the selected data contains labels.
Mann-Whitney test: Enable this option to perform the Mann-Whitney test.
Alternative Hypothesis: Select the alternative hypothesis to be used for the test.
Hypothesized Difference (D): Enter the value of the supposed difference between the samples.
Significance Level (%): Enter the significance level for the test (default value: 5\%5%).
p-value: Choose between the asymptotic, exact, or Monte Carlo methods. For the exact and Monte Carlo methods, you can specify the maximum time you want to spend computing the p-value.
Continuity correction: Activate this option if you want XLSTAT to use the continuity correction when computing the asymptotic p-value.
What are the results for the Mann-Whitney test in XLSTAT?
XLSTAT offers several outputs in the dialog box of the Mann-Whitney test. Here is a description:
Descriptive statistics: Check this option to display the descriptive statistics for the selected samples.
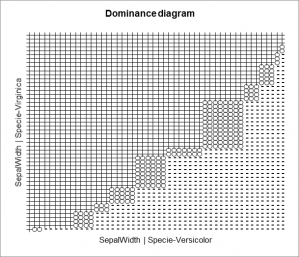
Dominance diagram: Check this option to display a dominance diagram in order to allow visual comparison of the samples.
Distributions: Activate this option to display the distributions.
Comparison plots: Activate this option to display the comparison plots (box plots, scattergrams, strip plots, bar charts).
In addition to the above outputs, XLSTAT displays a table with the results of the test such as the U statistic and the p-value:

Example of a Mann-Whitney test in XLSTAT
Our tutorial will help you perform and interpret a Mann-Whitney test for two independent samples in Excel using XLSTAT.

