Multidimensional tests (Mahalanobis, …)
Multidimensional tests allow to compare samples based on several variables. Available in Excel using the XLSTAT add-on statistical software.
What are multidimensional tests
Multidimensional tests implemented in XLSTAT are used to compare samples described by several variables. Instead of comparing the average of two samples as with the Student t test, we compare here simultaneously for the same samples averages measured for several variables.
Compared to a procedure that would involve as many Student t-tests as there are variables, the method proposed here has the advantage of using the structure of covariance of the variables and of obtaining an overall conclusion. It may be that two samples are different for a variable with a Student t test, but that overall it is impossible to reject the hypothesis that they are similar.
Mahalanobis distance
The Mahalanobis distance allows computing the distance between two points in a p-dimensional space, while taking into account the covariance structure across the p dimensions.
The square of the Mahalanobis distance writes:
dM² = (x1 - x2) ∑-1 (x1 - x2)
where xi is the vector x1 and ∑ is the covariance matrix.
The Mahalanobis distance can be used to compare two groups (or samples) because the Hotelling T² statistic defined by:
T² = [(n1*n2) ⁄ (n1 + n2)] dM
follows a Hotelling distribution, if the samples are normally distributed for all variables.
The F statistic that is used for the comparison test where the null hypothesis H0 is that the means of the two samples are equal, is defined by:
F = T² [n1+ n2 – (p-1)] ⁄ [(n1 + n2 – 2)*p]
This statistic follows a Fisher’s F distribution with p and n1+n2-p-1 degrees of freedom if the samples are normally distributed for all the variables.
If we want to compare more than two samples, the test based on the Mahalanobis distance can be used to identify possible sources of the difference observed at the global level. It is then recommended to use the Bonferroni correction for the alpha significance level.
Wilks’ lambda
Wilks' lambda is a statistical test used in multivariate analysis of variance to test whether there are differences between the means of the samples on a combination of dependent variables.
Testing the equality of the within-groups covariance matrices
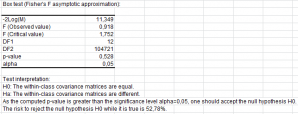
Box test
The Box test is used to test the assumption of equality for intra-class covariance matrices. Two approximations are available, one based on the Chi² distribution, and the other on the Fisher distribution.
Kullback’s test
The Kullback’s test is used to test the assumption of equality for intra-class covariance matrices. The statistic calculated is approximately distributed according to a Chi² distribution.

