Conditional Logit model
The conditional logit model is similar to logistic regression but incorporates dependency in the data. Available in Excel using the XLSTAT software.
Conditional Logit model definition
The conditional logit model introduced by McFadden (1973) is based on a model similar to the logistic regression. The difference is that all individuals are subjected to different situations before expressing their choice (modeled using a binary variable which is the dependent variable). The fact that the same individuals are used in taken in account by the conditional logit model .
(NB: the observations are not independent within a block corresponding to the same individual).
The conditional logit model is a method mostly used in conjoint analysis, it is nevertheless useful when analyzing a certain type of data.
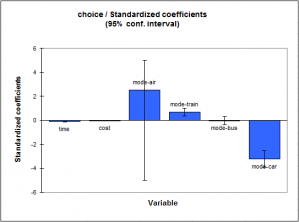
Instead of having one line per individual like in the classical logit model, there will be one row for each category of the variable of interest, per individual. If one seeks to study transportations, for example, there will be four types of transports (car / train / plane / bike), each type of transport having its own characteristics (their price, their environmental costs...) but an individual can choose only one of four transportations. As part of a conditional logit model, all four options are presented to each individual and the individual choose his preferred option. We have for N individuals, N * 4 rows with 4 rows for each individual associated with each transportation. The binary response variable will indicate the choice of the individual (1) and 0 if the individual did not choose this option.
In XLSTAT-Conjoint, you will also have to select a column associated with the name of the individuals (with 4 lines per individual in our example). The explanatory variables will also have N * 4 lines.
Conditional Logit model method
The conditional logit model is based on a model similar to that of the logistic regression except that instead of having individual characteristics, there will be characteristics of the different alternatives proposed to the individuals.
The probability that individual i chooses product j is given by:
Pij = eβTzij / ΣkeβTzik
From this probability, we calculate a likelihood function: l(β) = Σi=1..nΣj=1..J yij log(Pij)
With y being a binary variable indicating the choice of individual i for product j and J being the number of choices available to each individual.
To estimate the model parameters β (the coefficients of the linear function), it seeks to maximize the likelihood function. Unlike linear regression, an exact analytical solution does not exist. It is therefore necessary to use an iterative algorithm. XLSTAT-Conjoint uses a Newton-Raphson algorithm.

