Discriminant Analysis (DA)
Discriminant analysis is a popular explanatory and predictive data analysis technique that uses a qualitative variable as an output. Available in Excel using the XLSTAT software.
What is Discriminant Analysis?
Discriminant Analysis (DA) is a statistical method that can be used in explanatory or predictive frameworks:
- Check on a two or three-dimensional chart if the groups to which observations belong are distinct;
- Show the properties of the groups using explanatory variables;
- Predict which group a new observation will belong to.
Discriminant Analysis may be used in numerous applications, for example in ecology and the prediction of financial risks (credit scoring).
What is the difference between Linear and Quadratic Discriminant Analysis?
Two models of Discriminant Analysis are used depending on a basic assumption: if the covariance matrices are assumed to be identical, linear discriminant analysis is used. If, on the contrary, it is assumed that the covariance matrices differ in at least two groups, then the quadratic discriminant analysis should be preferred. The Box test is used to test this hypothesis (the Bartlett approximation enables a Chi2 distribution to be used for the test). It is common to start with linear analysis then, depending on the results from the Box test, to carry out quadratic analysis if required.
Discriminant Analysis and Multicollinearity issues
With linear and still more with quadratic models, we can face problems of variables with a null variance or multicollinearity between variables. XLSTAT has been programmed in a way to avoid these problems. The variables responsible for these problems are automatically ignored either for all calculations or, in the case of a quadratic model, for the groups in which the problems arise. Multicollinearity statistics are optionally displayed so that you can identify the variables which are causing problems.
Discriminant Analysis and variable selection
As for linear and logistic regression, efficient stepwise methods have been proposed. They can, however, only be used when quantitative variables are selected as the input and output tests on the variables assume them to be normally distributed. The stepwise method gives a powerful model which avoids variables which contribute only little to the model
Discriminant analysis and logistic regression
Where there are only two classes to predict for the dependent variable, discriminant analysis is very much like logistic regression. Discriminant analysis is useful for studying the covariance structures in detail and for providing a graphic representation. Logistic regression has the advantage of having several possible model templates, and enabling the use of stepwise selection methods including for qualitative explanatory variables. The user will be able to compare the performances of both methods by using the ROC curves.
Options of the Discriminant Analysis function in XLSTAT
- Equality of covariance matrices: Activate this option if you want to assume that the covariance matrices associated with the various classes of the dependent variable are equal (i.e. Linear Discriminant Analysis) or unequal (Quadratic Discriminant Analysis).
- Prior probabilities: Activate this option if you want to take prior possibilities into account. The probabilities associated with each of the classes are equal to the frequency of the classes. Note: this option has no effect if the prior possibilities are equal for the various groups.
- Model selection: Activate this option if you want to use one of the four selection methods provided:
Stepwise (Forward): The selection process starts by adding the variable with the largest contribution to the model. If a second variable is such that its entry probability is greater than the entry threshold value, then it is added to the model. After the third variable is added, the impact of removing each variable present in the model after it has been added is evaluated. If the probability of the calculated statistic is greater than the removal threshold value, the variable is removed from the model.
Stepwise (Backward): This method is similar to the previous one but starts from a complete model.
Forward: The procedure is the same as for stepwise selection except that variables are only added and never removed.
Backward: The procedure starts by simultaneously adding all variables. The variables are then removed from the model following the procedure used for stepwise selection.
Classes weight correction: If the number of observations for the various classes for the dependent variables are not uniform, there is a risk of penalizing classes with a low number of observations in establishing the model. To get over this problem, XLSTAT has two options:
Automatic: Correction is automatic. Artificial weights are assigned to the observations in order to obtain classes with an identical sum of weights.
Corrective weights: You can select the weights to be assigned to each observation.
Validation: Activate this option if you want to use a sub-sample of the data to validate the model.
Results of the Discriminant Analysis function in XLSTAT
- Classification table, ROC curve and cross-validation :
Among the numerous results provided, XLSTAT can display the classification table (also called confusion matrix) used to calculate the percentage of well-classified observations. When only two classes (or categories or modalities) are present in the dependent variable, the ROC curve may also be displayed. The ROC curve (Receiver Operating Characteristics) displays the performance of a model and enables a comparison to be made with other models. The terms used come from signal detection theory.
The proportion of well-classified positive events is called the sensitivity. The specificity is the proportion of well-classified negative events. If you vary the threshold probability from which an event is to be considered positive, the sensitivity and specificity will also vary. The curve of points (1-specificity, sensitivity) is the ROC curve. Let's consider a binary dependent variable which indicates, for example, if a customer has responded favorably to a mail shot. In the diagram below, the blue curve corresponds to an ideal case where the n% of people responding favorably corresponds to the n% highest probabilities. The green curve corresponds to a well-discriminating model. The red curve (first bisector) corresponds to what is obtained with a random Bernoulli model with a response probability equal to that observed in the sample studied. A model close to the red curve is therefore inefficient since it is no better than random generation. A model below this curve would be disastrous since it would be less even than random.
The area under the curve (or AUC) is a synthetic index calculated for ROC curves. The AUC corresponds to the probability such that a positive event has a higher probability given to it by the model than a negative event. For an ideal model, AUC=1 and for a random model, AUC = 0.5. A model is usually considered good when the AUC value is greater than 0.7. A well-discriminating model must have an AUC of between 0.87 and 0.9. A model with an AUC greater than 0.9 is excellent.
The results of the model as regards forecasting may be too optimistic: we are effectively trying to check if an observation is well-classified while the observation itself is being used in calculating the model. For this reason, cross-validation was developed: to determine the probability that an observation will belong to the various groups, it is removed from the learning sample, then the model and the forecast are calculated.
- Sum of weights, prior probabilities and logarithms of determinants for each class: These statistics are used, among other places, in the posterior calculations of probabilities for the observations.
- Multicollinearity: This table identifies the variables responsible for the multicolinearity between variables. As soon as a variable is identified as being responsible for a multicolinearity (its tolerance is less than the limit tolerance set in the "options" tab in the dialog box), it is not included in the multicolinearity statistics calculation for the following variables. Thus in the extreme case where two variables are identical, only one of the two variables will be eliminated from the calculations. The statistics displayed are the tolerance (equal to 1-R²), its inverse and the VIF (Variance inflation factor).
- SSCP matrices: The SSCP (Sums of Squares and Cross Products) matrices are proportional to the covariance matrices. They are used in the calculations and check the following relationship: SSCP total = SSCP inter + SSCP intra total.
- Covariance matrices: The inter-class covariance matrix (equal to the unbiased covariance matrix for the means of the various classes), the intra-class covariance matrix for each of the classes (unbiased), the total intra-class covariance matrix, which is a weighted sum of the preceding ones, and the total covariance matrix calculated for all observations (unbiased) are displayed successively.
- Box test: The Box test is used to test the assumption of equality for intra-class covariance matrices. Two approximations are available, one based on the Chi2 distribution, and the other on the Fisher distribution. The results of both tests are displayed.
- Kullback’s test: The Kullback’s test is used to test the assumption of equality for intra-class covariance matrices. The statistic calculated is approximately distributed according to a Chi2 distribution.
- Mahalanobis distances: The Mahalanobis distance is used to measure the distance between classes taking account of the covariance structure. If we assume the intra-class variance matrices are equal, the distance matrix is calculated by using the total intra-class covariance matrix which is symmetric. If we assume the intra-class variance matrices are not equal, the Mahalanobis distance between classes i and j is calculated by using the intra-class covariance matrix for class i which is symmetric. The distance matrix is therefore asymmetric.
- Fisher’s distances: If the covariance matrices are assumed to be equal, the Fisher distances between the classes are displayed. They are calculated from the Mahalanobis distance and are used for a significance test. The matrix of p-values is displayed so as to identify which distances are significant.
- Generalized squared distances: If the covariance matrices are not assumed to be equal, the table of generalized squared distances between the classes is displayed. The generalized distance is also calculated from the Mahalanobis distances and uses the logarithms of the determinants of the covariance matrices together with the logarithms of the prior probabilities if required by the user.
- Wilks’ Lambda test (Rao’s approximation): The test is used to test the assumption of equality of the mean vectors for the various classes. When there are two classes, the test is equivalent to the Fisher test mentioned previously. If the number of classes is less than or equal to three, the test is exact. The Rao approximation is required from four classes to obtain a statistic approximately distributed according to a Fisher distribution.
- Unidimensional test of equality of the means of the classes: These tests are used to test the assumption of equality of the means between classes variable by variable. Wilks’ univariate lambda is always between 0 and 1. A value of 1 means the class means are equal. A low value is interpreted as meaning there are low intra-class variations and therefore high inter-class variations, hence a significant difference in class means.
- Pillai’s trace: The test is used to test the assumption of equality of the mean vectors for the various classes. It is less used than Wilks’ Lambda test and also uses the Fisher distribution for calculating p-values.
- Hotelling-Lawley trace: The test is used to test the assumption of equality of the mean vectors for the various classes. It is less used than Wilks’ Lambda test and also uses the Fisher distribution for calculating p-values.
- Roy’s greatest root: The test is used to test the assumption of equality of the mean vectors for the various classes. It is less used than Wilks’ Lambda test and also uses the Fisher distribution for calculating p-values.
- Eigenvalues: This table shows the eigenvalues associated with the various factors together with the corresponding discrimination percentages and cumulative percentages. In discriminant analysis, the number of non-null eigenvalues is equal to at most (k-1) where k is the number of classes. The scree plot is used to display how the discriminant power is distributed between the discriminant factors. The sum of the eigenvalues is equal to the Hotelling trace.
- Bartlett’s test on significancy of eigenvalues: This table displays for each eigenvalue, the Bartlett statistic and the corresponding p-value which is computed using the asymptotic Chi-square approximation. The Bartlett’s test allows to test the null hypothesis H0 that all the p eigenvalues are equal to zero. If it is rejected for the greatest eigenvalue then the test is performed again until H0 cannot be rejected. This test is known as conservative, meaning that it tends to confirm H0 in some cases where it should not. You can however use this test to check how many factorial axes you should consider (see Jobson, 1992).
- Eigenvectors: This table shows the eigenvectors afterwards used in the canonical correlations, canonical function coefficients and observation coordinate (scores) calculations.
- Variables/Factors correlations: The calculation of correlations between the scores in the initial variable space and in the discriminant factor space is used to display the relationship between the initial variables and the factors in a correlation circle. The correlation circle is an aid in interpreting the representation of the observations in factor space.
- Canonical correlations: The canonical correlations associated with each factor are the square roots of L(i) / (1- L(i)) where L(i) is the eigenvalue associated with factor i. Canonical correlations are also a measurement of the discriminant power of the factors. Their sum is equal to the Pilai’s trace.
- Canonical discriminant function coefficients: These coefficients can be used to calculate the coordinates of an observation in discriminant factor space from its coordinates in the initial variable space.
- Standardized canonical discriminant function coefficients: These coefficients are the same as the previous, but are standardized. Thus comparing them gives a measure of the relative contribution of the initial variables to the discrimination for a given factor.
- Functions at the centroids: This table gives the evaluation of the discriminant functions for the mean points for each of the classes.
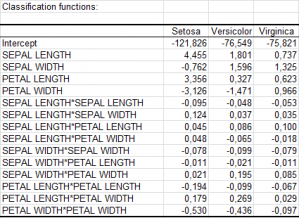
- Classification functions: The classification functions can be used to determine which class an observation is to be assigned to using values taken for the various explanatory variables. If the covariance matrices are assumed equal, these functions are linear. If the covariance matrices are assumed unequal, these functions are quadratic. An observation is assigned to the class with the highest classification function.
- Prior and posterior classification, membership probabilities, scores and squared distances: This table shows for each observation its membership class defined by the dependent variable, the membership class as deduced by the membership probabilities, the probabilities of membership of each of the classes, the coordinates in discriminant factor space and the squared distances of the observations from the centroids of each of the classes.
- Confusion matrix for the estimation sample: The confusion matrix is deduced from prior and posterior classifications together with the overall percentage of well-classified observations. Where the dependent variable only comprises two classes, the ROC curve is displayed.
- Cross-validation: Where cross-validation has been requested, the table containing the information for the observations and the confusion matrix are displayed.
Discriminant Analysis charts in XLSTAT
- Correlation charts: Activate this option to display the charts involving correlations between the factors and input variables.
Vectors: Activate this option to display the input variables with vectors.

Observations charts: Activate this option to display the charts that allow visualizing the observations in the new space.
Labels: Activate this option to display the observations labels on the charts. The number of labels can be modulated using the filtering option.
Display the centroids: Activate this option to display the centroids that correspond to the categories of the dependent variable.
Confidence ellipses: Activate this option to display confidence ellipses. The confidence ellipses correspond to a x% confidence interval (where x is determined using the significance level entered in the Options tab) for a bivariate normal distribution with the same means and the same covariance matrix as the factor scores for each category of the dependent variable.
Use covariance hypothesis: Activate this option to base the computation of the ellipses on the hypothesis that covariance matrices are equal or not.

- Centroids and confidence circles: Activate this option to display a chart with the centroids and the confidence circles around the means.
Discriminant Analysis tutorial in XLSTAT
This tutorial will help you set up and interpret a Discriminant Analysis in Excel using XLSTAT.


analyze your data with xlstat
Related features