Régression linéaire
Utilisez ce module pour créer un modèle de régression linéaire simple ou multiple dans un but explicatif ou prédictif. Disponible dans Excel avec le logiciel XLSTAT.
Qu'est-ce que la régression linéaire?
La régression linéaire est sans aucun doute la méthode de modélisation statistique la plus utilisée. On distingue habituellement la régression simple (une seule variable explicative) de la régression multiple (plusieurs variables explicatives) bien que le cadre conceptuel et les méthodes de calcul soient identiques.
Le principe de la régression linéaire est de modéliser une variable dépendante quantitative Y, au travers d'une combinaison linéaire de p variables explicatives quantitatives, X1, X2, …, Xp. L'équation linéaire du modèle s'écrit pour une observation i :
yi = a1x1i + a2x2i + ... + apxpi + ei
où yi est la valeur observée pour la variable dépendante pour l'observation i, xij est la valeur prise par la variable j pour l'observation i, et ei est l'erreur du modèle.
Le cadre statistique et les hypothèses qui l'accompagnent ne sont pas nécessaires pour ajuster ce modèle. Comme la minimisation par la méthode des moindres carrés (on minimise la somme des erreurs quadratiques e²i) fournit une solution analytique exacte, nous pouvons nous demander : les moindres carrés (OLS) et la régression linéaire représentent-ils la même chose ? La réponse est non, puisqu'OLS est seulement la méthode qui permet de trouver l'équation de la droite de régression linéaire.
Les hypothèses de la régression linéaire sont les suivantes : les erreurs ei suivent une même loi normale N(0,s) et sont indépendantes. Si l'on veut pouvoir tester des hypothèses et mesurer le pouvoir explicatif des différentes variables explicatives dans le modèle, un cadre statistique est nécessaire.
Allez plus loin : sélectionner les variables dans XLSTAT
Toutes les variables ne sont pas importantes ou significatives pour le modèle de régression. XLSTAT permet de sélectionner seulement les variables les plus importantes qui font partie du modèle final. Quatre méthodes sont disponibles dans XLSTAT :
- Meilleur modèle : cette méthode permet de choisir le meilleur modèle parmi tous les modèles comprenant un nombre de variables variant de « Min variables » à « Max variables ». Par ailleurs, le « critère » pour déterminer le meilleur modèle peut être choisi par l'utilisateur. Le critère peut être choisi parmi les suivants : R² ajusté, Moyenne des Carrés des Erreurs (MCE), Cp de Mallows, AIC de Akaike, SBC de Schwarz, PC d'Amemiya.
- Stepwise ou Progressive : le processus de sélection commence par l'ajout de la variable ayant la plus forte contribution au modèle (le critère utilisé est la statistique t de Student). Si une seconde variable est telle que la probabilité associée à son t est inférieure à la « Probabilité pour l'entrée », elle est ajoutée au modèle. De même pour une troisième variable. À partir de l'ajout de la troisième variable, après chaque ajout, on évalue pour toutes les variables présentes dans le modèle quel serait l'impact de son retrait (toujours au travers de la statistique t). Si la probabilité est supérieure à la « Probabilité pour le retrait », la variable est retirée. La procédure se poursuit jusqu'à ce que plus aucune variable ne puisse être ajoutée/retirée.
- Ascendante : la procédure est identique à celle de la sélection progressive, sauf que les variables sont uniquement ajoutées et jamais retirées.
- Descendante : la procédure commence par l'ajout simultané de toutes les variables. Les variables sont ensuite retirées du modèle suivant la procédure utilisée pour la sélection progressive.
Comment vérifier les hypothèses de la régression linéaire ?
Il faut vérifier deux hypothèses principales concernant les résidus avant de réaliser une régression linéaire :
- ils doivent suivre une distribution normale
- ils doivent être indépendants
Utilisez les différents tests proposés dans les résultats de la régression linéaire pour vérifier a posteriori que les hypothèses sous-jacentes ont été correctement vérifiées.
La normalité des résidus peut être vérifiée par l'analyse de certaines graphiques ou en utilisant le test de Shapiro-Wilk (option disponible dans le sous-onglet Test des hypothèses).
L'indépendance des résidus peut être vérifiée par l'analyse de certaines graphiques ou en utilisant le test de Durbin-Watson.
Comment corriger l'hétéroscédasticité et l'autocorrélation ?
Comme spécifié précédemment, l'homoscédasticité et l'indépendance des résidus (termes d'erreur) sont des hypothèses clefs de la régression, où, pour rappel, on suppose qu'ils sont indépendants, identiquement distribués suivant une loi normale de moyenne nulle et de variance fixe. XLSTAT permet de corriger les matrices de covariance pour les effets d'hétéroscédasticité et d'autocorrélation qui peuvent survenir notamment dans des cas où le temps intervient (séries chronologiques, données longitudinales).
Différentes méthodes sont proposées dans XLSTAT pour ces corrections, comme l'estimateur suggéré par Newey et West (1987).
Quels résultats de la régression linéaire sont disponibles dans XLSTAT ?
Ci-dessous est une liste non exhaustive des résultats obtenus pour la régression linéaire avec XLSTAT.
- Synthèse de la sélection de variables : quand une méthode de sélection a été choisie, XLSTAT affiche la synthèse de la sélection. Pour une sélection pas à pas, les différentes étapes sont affichées. Quand le meilleur modèle pour un nombre de variables variant de p à q a été sélectionné, le meilleur modèle pour chaque nombre de variables est affiché avec les statistiques de test correspondantes et le meilleur modèle selon le critère choisi est affiché en gras.
- Coefficients d'ajustement : dans ce tableau sont affichées les statistiques relatives à l'ajustement du modèle de régression :
- Observations : le nombre d'observations prises en compte dans les calculs.
- Somme des poids : la somme des poids des observations prises en compte dans les calculs.
- DDL : le nombre de degrés de liberté pour le modèle retenu (correspondant à la partie erreurs).
- R² : le coefficient de détermination du modèle. Le R² s'interprète comme la proportion de la variabilité de la variable dépendante expliquée par le modèle. Plus le R² est proche de 1, meilleur est le modèle. L'inconvénient du R² est qu'il ne prend pas en compte le nombre de variables utilisées pour ajuster le modèle.
- R² ajusté : le coefficient de détermination ajusté du modèle. Le R² ajusté peut être négatif si le R² est voisin de zéro. Le R² ajusté est une correction du R² qui permet de prendre en compte le nombre de variables utilisées dans le modèle.
- MCE : la moyenne des carrés des erreurs (MCE).
- RMCE : la racine de la moyenne des carrés des erreurs (RMCE) est la racine carrée de la MCE.
- MAPE : la Mean Absolute Percentage Error.
- DW : Le coefficient de Durbin-Watson. Ce coefficient correspond au coefficient d'autocorrélation d'ordre 1 et permet de vérifier que les résidus du modèle ne sont pas autocorrélés, sachant que l'indépendance des résidus est l'une des hypothèses de base de la régression linéaire. L'utilisateur pourra se référer à une table des coefficients de Durbin-Watson pour vérifier si l'hypothèse d'indépendance des résidus est acceptable.
- Cp : le coefficient Cp de Mallows.
- AIC : le critère d'information d'Akaike (Akaike's Information Criterion). Ce critère proposé par Akaike (1973) dérive de la théorie de l'information, et s'appuie sur la mesure de Kullback et Leibler (1951). C'est un critère de sélection de modèles qui pénalise les modèles pour lesquels l'ajout de nouvelles variables explicatives n'apporte pas suffisamment d'informations au modèle, l'information étant mesurée au travers de la SCE. On cherche à minimiser le critère AIC.
- SBC : le critère bayésien de Schwarz (Schwarz's Bayesian Criterion). Ce critère proposé par Schwarz (1978) est proche du critère AIC, et comme ce dernier on cherche à le minimiser.
- PC : le critère de prédiction d'Amemiya (Amemiya's Prediction Criterion). Ce critère proposé par Amemiya (1980) permet comme le R² ajusté de tenir compte de la parcimonie du modèle.
- Press RMCE : le Press RMCE peut alors être comparé au RMCE. Une différence importante entre les deux indique que le modèle est sensible à la présence ou absence de certaines observations dans le modèle.
- Le tableau des Type I SS permet de visualiser l'influence de l'ajout progressif des variables explicatives sur l'ajustement du modèle, au sens de la somme des carrés des erreurs (SCE), de la moyenne des carrés des erreurs (MCE), du F de Fisher, ou de la probabilité associée au F de Fisher. Plus la probabilité est faible, plus la contribution de la variable au modèle est importante, toutes les autres variables étant déjà dans le modèle. Remarque : l'ordre de sélection des variables dans le modèle influe sur les valeurs obtenues.
- Le tableau des Type II SS permet de visualiser l'influence du retrait d'une variable explicative sur l'ajustement du modèle, toutes les autres variables étant conservées, au sens de la somme des carrés des erreurs (SCE), de la moyenne des carrés des erreurs (MCE), du F de Fisher, ou de la probabilité associée au F de Fisher. Plus la probabilité est faible, plus la contribution de la variable au modèle est importante. Remarque : dans le cas des ANOVAs déséquilibrées, l'utilisation des Type III est recommandée, mais XLSTAT affiche les Type II pour les utilisateurs avancés qui souhaiteraient disposer des Type II.
- Le tableau des Type III SS permet de visualiser l'influence du retrait d'une variable explicative sur l'ajustement du modèle, toutes les autres variables étant conservées, au sens de la somme des carrés des erreurs (SCE), de la moyenne des carrés des erreurs (MCE), du F de Fisher, ou de la probabilité associée au F de Fisher. Plus la probabilité est faible, plus la contribution de la variable au modèle est importante, toutes les autres variables étant déjà dans le modèle. Remarque : contrairement au cas des Type I SS, l'ordre de sélection des variables dans le modèle n'influe pas sur les valeurs obtenues, et contrairement aux Type II SS, les valeurs ne dépendent pas des effectifs des cellules (par cellule, on entend une combinaison de modalités des différents facteurs), ce qui fait des Type III le test recommandé pour évaluer la contribution d'une variable.
- Le tableau d'analyse de la variance permet d'évaluer le pouvoir explicatif des variables explicatives. Dans le cas où la constante du modèle n'est pas fixée à une valeur donnée, le pouvoir explicatif est évalué en comparant l'ajustement (au sens des moindres carrés) du modèle final avec l'ajustement du modèle rudimentaire composé d'une constante égale à la moyenne de la variable dépendante. Dans le cas où la constante du modèle est fixée, la comparaison est faite par rapport au modèle pour lequel la variable dépendante serait égale à la constante fixée.
- L'équation du modèle est ensuite affichée pour faciliter la lecture ou la réutilisation du modèle.
- Le tableau des coefficients normalisés (aussi appelés coefficients bêta) permet de comparer le poids relatif des variables. Plus la valeur absolue d'un coefficient est élevée, plus le poids de la variable correspondante est important. Lorsque l'intervalle de confiance autour des coefficients normalisés comprend la valeur 0 (cela est facilement visible sur le graphique des coefficients normalisés), le poids d'une variable dans le modèle n'est pas significatif.
- Dans le tableau des prédictions et résidus sont donnés pour chaque observation, son poids, la valeur de la variable explicative qualitative s'il n'y en a qu'une, la valeur observée de la variable dépendante, la prédiction du modèle, les résidus, les résidus studentisés, les intervalles de confiance, ainsi que la prédiction ajustée si l'option correspondante a été activée dans la boîte de dialogue. Deux types d'intervalles de confiance sont affichés : un intervalle de confiance autour de la moyenne (correspondant au cas où l'on ferait la prédiction pour un nombre infini d'observations avec un ensemble de valeurs données des variables explicatives) et un intervalle autour de la prédiction ponctuelle (correspondant au cas d'une prédiction isolée pour des valeurs données des variables explicatives). Le second intervalle est toujours plus grand que le premier, l'incertitude étant plus importante. Si des données de validation ont été sélectionnées, elles sont affichées en fin de tableau.
- Dans le tableau des diagnostics d'influence sont affichés pour chaque observation, son poids, le résidu, le résidu normalisé (division par la RMCE), le résidu studentisé, le résidu supprimé (Deleted), le résidu supprimé studentisé, le leverage, la distance de Mahalanobis, le D de Cook, le CovRatio, le DFFits, le DFFits standardisé, les DFBeta (un par coefficient du modèle) et les DFBeta standardisés.
Résultats graphiques pour la régression linéaire
Les graphiques suivants permettent de visualiser les résultats mentionnés ci-dessus.
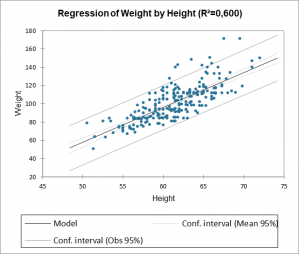
S'il n'y a qu'une seule variable explicative dans le modèle, le premier graphique affiché permet de visualiser les valeurs observées, la droite de régression et les deux types d'intervalles de confiance autour des prévisions.
Le second graphique permet quant à lui de visualiser les résidus normalisés en fonction de la variable explicative. En principe, les résidus doivent être distribués de manière aléatoire autour de l'axe des abscisses. L'observation d'une tendance ou d'une forme révélerait un problème au niveau du modèle.
Les trois graphiques affichés ensuite permettent de visualiser respectivement l'évolution des résidus normalisés en fonction de la variable dépendante, la distance entre les prédictions et les observations (pour un modèle idéal, les points seraient tous sur la bissectrice), et les résidus normalisés sur la forme d'un diagramme en bâtons. Ce dernier graphique permet de rapidement voir si un nombre anormal de données sort de l'intervalle ]-2, 2[ sachant que ce dernier, sous hypothèse de normalité, doit contenir environ 95% des données.


analysez vos données avec xlstat
Fonctionnalités corollaires